Question

已知数列的前n项和，数列的前n项和，，
（1）求，的通项公式；
（2）设，是否存在正整数,使得对恒成立？若存在，求出的值；若不存在，说明理由。

Answer 1

（1）①，，  ，。
（2）存在正整数3，使得对恒成立。

本题考查等差数列和等比数列的通项公式的和对数的运算法则，特别是问题（2）的设置有新意，关键是恒等式的解题方法（对应系数相等）是解题的关键，属中档题．
（1）根据前n项和与通项公式的关系可知
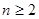
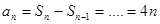
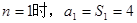
①时，；；综上，，
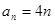
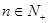
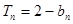
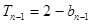
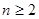
②由，，（）两式相减得
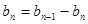
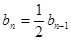
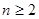
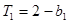
即，；由得，
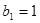
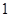
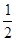
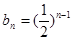
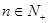
∴是以为首项，公比为的等比数列，，得到结论。
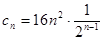
（2）因为，那么利用定义判定单调性，进而得到最值。
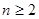
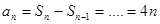
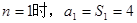
解：（1）①时，；；综上，，
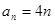
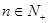
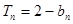
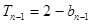
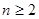
②由，，（）两式相减得
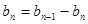
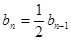
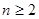
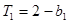
即，；由得，
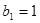
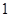
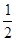
∴是以为首项，公比为的等比数列，，。
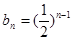
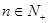
（2），
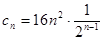
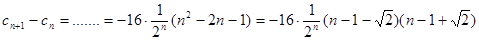
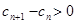
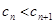
∴时，， ，即；
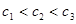
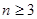
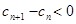
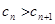
时，，，即
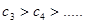
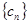
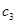
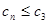
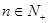
∴的最大项为，即存在正整数3，使得对恒成立。