
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 在
在![]() 上是单调增函数,求实数
上是单调增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)求出函数的定义域以及导数,结合定义域,讨论![]() 和
和![]() 情况下,导数的正负,即可得到
情况下,导数的正负,即可得到![]() 的单调性;
的单调性;
(2)求出![]() ,则
,则![]() 在
在![]() 上是单调增函数等价于
上是单调增函数等价于![]() 在
在![]() 上恒成立,分离参数
上恒成立,分离参数![]() ,即
,即![]() 在
在![]() 恒成立,令
恒成立,令![]() ,
,
利用导数求出函数![]() 在
在![]() 上的最大值,即可得到实数
上的最大值,即可得到实数![]() 的取值范围
的取值范围
(1)函数![]() ,则函数
,则函数![]() 的定义域为
的定义域为![]() .
.
![]()
①当![]() 时,
时,![]() 故函数
故函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,在
时,在 有
有![]() 故
故![]() 在
在![]() 单调递减;
单调递减;
在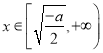 有
有![]() 故
故![]() 在
在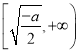 上单调递增。
上单调递增。
综上所述:当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上为单调递减,在
上为单调递减,在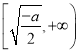 上为单调递减增
上为单调递减增
(2)由![]() ,得
,得![]() .
.
若函数![]() 为
为![]() 上的单调增函数,则
上的单调增函数,则![]() 在
在![]() 上恒成立,
上恒成立,
即不等式![]() 在
在![]() 上恒成立.也即
上恒成立.也即![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,
![]()
![]() 在
在![]() 上为减函数,则
上为减函数,则![]()
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 若满足:①对任意
若满足:①对任意![]() 、
、![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“中心捺函数”,其中点
为“中心捺函数”,其中点![]() 称为函数
称为函数![]() 的中心.已知函数
的中心.已知函数![]() 是以
是以![]() 为中心的“中心捺函数”,若满足不等式
为中心的“中心捺函数”,若满足不等式![]() ,当
,当![]() 时,
时,![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台机床生产的零件各100件进行检测,检测结果统计如下:
测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
甲机床 | 8 | 12 | 40 | 32 | 8 |
乙机床 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产1件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元,假设甲机床某天生产50件零件,请估计甲机床该天的利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任意抽取2件进行质量分析,求这2件都是乙机床生产的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”; ③“
”; ③“![]() ,则
,则![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域和值域均为[-a,a]的函数y=![]() 和y=g(x)的图象如图所示,其中a>c>b>0,给出下列四个结论正确结论的是( )
和y=g(x)的图象如图所示,其中a>c>b>0,给出下列四个结论正确结论的是( )
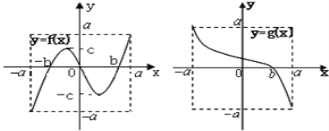
A.方程f[g(x)]=0有且仅有三个解B.方程g[f(x)]=0有且仅有三个解
C.方程f[f(x)]=0有且仅有九个解D.方程g[g(x)]=0有且仅有一个解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com