
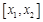 上的函数
上的函数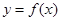 的图象为
的图象为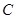 ,
,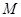 是
是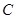 上的任意一点,
上的任意一点,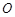 为坐标原点,设向量
为坐标原点,设向量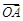 =
=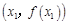 ,
,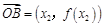 ,
,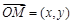 ,当实数λ满足x="λ" x1+(1-λ) x2时,记向量
,当实数λ满足x="λ" x1+(1-λ) x2时,记向量 =λ
=λ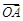 +(1-λ)
+(1-λ) .定义“函数
.定义“函数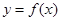 在区间
在区间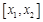 上可在标准
上可在标准 下线性近似”是指 “
下线性近似”是指 “
 恒成立”,其中
恒成立”,其中 是一个确定的正数.
是一个确定的正数.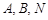 三点共线;
三点共线; 在区间[0,1]上可在标准
在区间[0,1]上可在标准 下线性近似,求
下线性近似,求 的取值范围;
的取值范围;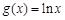 在区间
在区间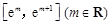 上可在标准
上可在标准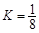 下线性近似.
下线性近似.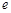 =2.718,
=2.718,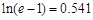 )
) =λ
=λ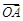 +(1-λ)
+(1-λ) 得到
得到 =λ
=λ ,所以B,N,A三点共线。
,所以B,N,A三点共线。 .(3)见解析。
.(3)见解析。 =λ
=λ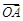 +(1-λ)
+(1-λ) 得到
得到 =λ
=λ ,所以B,N,A三点共线。 ………… 2分
,所以B,N,A三点共线。 ………… 2分 =λ
=λ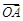 +(1-λ)
+(1-λ) ,得N与M的横坐标相同.…4分
,得N与M的横坐标相同.…4分 ,故
,故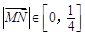 ;
; . …………………………………………… 6分
. …………………………………………… 6分 上的函数
上的函数 ,A(
,A(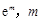 ),B(
),B( ),
),  , ………………………………………………8分
, ………………………………………………8分 ,其中
,其中 ,于是
,于是 , …10分
, …10分| x | em | (em,em+1-em) | em+1-em | (em+1-em,em+1) | em+1 |
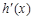 | | + | 0 | - | |
 | 0 | 增 | 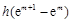 | 减 | 0 |
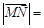
 ,且在
,且在 处取得最大值,
处取得最大值, 0.123
0.123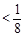 ,从而命题成立. …………………………………12分
,从而命题成立. …………………………………12分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:单选题
 所在平面内一点,且满足
所在平面内一点,且满足 ,则点O是
,则点O是 的( )
的( )| A.三条内角平分线交点(即内心) | B.三边的垂直平分线交 点(即外心) |
| C.三条高线的交点(即垂心) | D.三条中线交点(即重心) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com