
【题目】某学校组织高一、高二年级学生进行了“纪念建国70周年”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图和高二年级成绩的频数分布表.
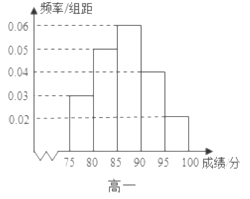
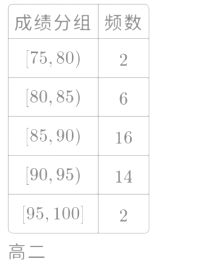
(Ⅰ)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(Ⅱ)在抽取的学生中,从成绩为[95,100]的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率;
(Ⅲ)记高一、高二两个年级知识竞赛的平均分分别为![]() ,试估计
,试估计![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
【答案】(Ⅰ)0.85(Ⅱ) ![]() .(Ⅲ)
.(Ⅲ) ![]() .
.
【解析】
(Ⅰ)利用对立事件概率计算公式能求出高一年级知识竞赛的达标率.(Ⅱ)高一年级成绩为[95,100]的有0.02×5×40=4名,记为A1,A2,A3,A4,高二年级成绩为[95,100]的有2名,记为B1,B2,利用列举法能求出2名学生来自于同一年级的概率.(Ⅲ)![]() .
.
(Ⅰ)高一年级知识竞赛的达标率为:![]() .
.
(Ⅱ)高一年级成绩为![]() 的有
的有![]() 名,记为
名,记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
高二年级成绩为![]() 的有2名,记为
的有2名,记为![]() ,
,![]() .
.
选取2名学生的所有可能为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15种;
,共15种;
其中2名学生来自于同一年级的有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共7种;
,共7种;
设2名学生来自于同一年级为事件![]() ,
,
所![]() .
.
(Ⅲ)![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,△ABC为正三角形,且BC=CD=2,CD⊥BC,将△ABC沿BC翻折.
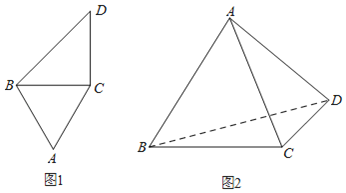
(1)当AD=2时,求证:平面ABD⊥平面BCD;
(2)若点A的射影在△BCD内,且直线AB与平面ACD所成角为60°,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,过焦点且垂直于x轴的直线被椭圆截得的线段长为3
,过焦点且垂直于x轴的直线被椭圆截得的线段长为3
(1)求椭圆的方程;
(2)已知P为直角坐标平面内一定点,动直线l:![]() 与椭圆交于A、B两点,当直线PA与直线PB的斜率均存在时,若直线PA与PB的斜率之和为与t无关的常数,求出所有满足条件的定点P的坐标.
与椭圆交于A、B两点,当直线PA与直线PB的斜率均存在时,若直线PA与PB的斜率之和为与t无关的常数,求出所有满足条件的定点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店制作并销售一款蛋糕,制作一个蛋糕成本3元,且以8元的价格出售,若当天卖不完,剩下的则无偿捐献给饲料加工厂。根据以往100天的资料统计,得到如下需求量表。该蛋糕店一天制作了这款蛋糕![]() 个,以
个,以![]() (单位:个,
(单位:个,![]() ,
,![]() )表示当天的市场需求量,
)表示当天的市场需求量,![]() (单位:元)表示当天出售这款蛋糕获得的利润.
(单位:元)表示当天出售这款蛋糕获得的利润.
需求量/个 |
|
|
|
|
|
天数 | 15 | 25 | 30 | 20 | 10 |
(1)当![]() 时,若
时,若![]() 时获得的利润为
时获得的利润为![]() ,
,![]() 时获得的利润为
时获得的利润为![]() ,试比较
,试比较![]() 和
和![]() 的大小;
的大小;
(2)当![]() 时,根据上表,从利润
时,根据上表,从利润![]() 不少于570元的天数中,按需求量分层抽样抽取6天.
不少于570元的天数中,按需求量分层抽样抽取6天.
(i)求此时利润![]() 关于市场需求量
关于市场需求量![]() 的函数解析式,并求这6天中利润为650元的天数;
的函数解析式,并求这6天中利润为650元的天数;
(ii)再从这6天中抽取3天做进一步分析,设这3天中利润为650元的天数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,长轴长为4,离心率为
,长轴长为4,离心率为![]() .过右焦点
.过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(均不与
两点(均不与![]() 重合),记直线
重合),记直线![]()
![]() 的斜率分别为
的斜率分别为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在常数![]() ,当直线
,当直线![]() 变动时,总有
变动时,总有![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,四边形ABCD为平行四边形,△PCD为正三角形,∠BAD=30°,AD=4,AB=2![]() ,平面PCD⊥平面ABCD,E为PC中点.
,平面PCD⊥平面ABCD,E为PC中点.
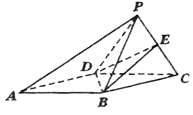
(1)证明:BE⊥PC;
(2)求多面体PABED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中开设大学先修课程已有两年,两年共招收学生2000人,其中有300人参与学习先修课程,两年全校共有优等生200人,学习先修课程的优等生有60人.这两年学习先修课程的学生都参加了考试,并且都参加了某高校的自主招生考试(满分100分),结果如下表所示:
分数 |
|
|
|
|
|
人数 | 20 | 55 | 105 | 70 | 50 |
参加自主招生获得通过的概率 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
(1)填写列联表,并画出列联表的等高条形图,并通过图形判断学习先修课程与优等生是否有关系,根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | |||
没有学习大学先修课程 | |||
总计 |
(2)已知今年有150名学生报名学习大学先修课程,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人,求他获得某高校自主招生通过的概率;
②设今年全校参加大学先修课程的学生获得某高校自主招生通过的人数为![]() ,求
,求![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年“双十一”当天,甲、乙两大电商进行了打折促销活动,某公司分别调查了当天在甲、乙电商购物的1000名消费者的消费金额,得到了消费金额的频数分布表如下:
甲电商:
消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
频数 | 50 | 200 | 350 | 300 | 100 |
乙电商:
消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
频数 | 250 | 300 | 150 | 100 | 200 |
(Ⅰ)根据频数分布表,完成下列频率分布直方图,并根据频率分布直方图比较消费者在甲、乙电商消费金额的中位数的大小以及方差的大小(其中方差大小给出判断即可,不必说明理由);
(Ⅱ)(ⅰ)根据上述数据,估计“双十一”当天在甲电商购物的大量的消费者中,消费金额小于3千元的概率;
(ⅱ)现从“双十一”当天在甲电商购物的大量的消费者中任意调查5位,记消费金额小于3千元的人数为X,试求出X的期望和方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com