Question

已知x，y满足

x-y+2≥0 x+y-4≥0 2x-y-5≤0

．
（1）求z=x²+y²+2x-2y+2的最小值；
（2）求z=|x+2y-4|的最大值．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：（1）z=x²+y²+2x-2y+2的几何意义为两点间的距离的平方，
（2）作出不等式组对应的平面区域利用z=|x+2y-4|的几何意义，即可求最大值；

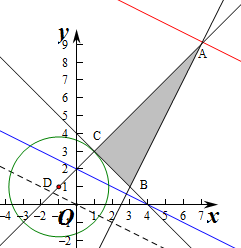
解答： 解：（1）画出不等式组所构成的平面区域如图中阴影部分．并求出顶点的坐标C（1，3）、B（3，1）、A（7，9）．
z=x²+y²+2x-2y+2=（x+1）²+（y-1）²表示阴影部分中的点（x，y）与点D（-1，1）距离的平方，
由图可知CD的距离最小此时z=（1+1）²+（3-1）²=4+4=8．
因此z的最小值是8．
（2）易知可行域内各点均在直线x+2y-4=0的上方，故x+2y-4＞0，
即z=|x+2y-4|=x+2y-4，
由z=x+2y-4，得y=-

1

2

x+

z

2

+2，平移直线y=-

1

2

x+

z

2

+2，由图象可知当直线经过点A时，
直线y=-

1

2

x+

z

2

+2的截距最大，此时z最大，
将点A（7，9）代入z得最大值为z=7+18-4=21．

点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．要求熟练掌握常见目标函数的几何意义．