
【题目】已知椭圆C:![]() 1(a>b>0)的离心率e
1(a>b>0)的离心率e![]() ,且点P(
,且点P(![]() ,1)在椭圆C上.
,1)在椭圆C上.
(1)求椭圆C的方程;
(2)若椭圆C的左焦点为F,右顶点为A,点M(s,t)(t>0)是椭圆C上的动点,直线AM与y轴交于点D,点E是y轴上一点,EF⊥DF,EA与椭圆C交于点G,若△AMG的面积为2![]() ,求直线AM的方程.
,求直线AM的方程.
【答案】(1)![]() (2)x
(2)x![]() y﹣2=0
y﹣2=0
【解析】
(1)利用离心率和椭圆经过的点建立方程组,可以求解方程;
(2)设出直线方程,联立方程组,结合三角形的面积为2![]() 可得直线斜率,从而可得方程.
可得直线斜率,从而可得方程.
(1)由题意得e![]() ,
,![]() ,a2=b2+c2,解得:a2=4,b2=2,
,a2=b2+c2,解得:a2=4,b2=2,
所以椭圆的方程:![]() .
.
(2)由(1)得左焦点F(![]() ,0),A(2,0),设直线AM:y=k(x﹣2),由题意得D(0,﹣2k),∴kDF
,0),A(2,0),设直线AM:y=k(x﹣2),由题意得D(0,﹣2k),∴kDF![]() k,
k,
∵EF⊥DF,∴kEF![]() ,∴直线EF的方程:x
,∴直线EF的方程:x![]() ,
,
令x=0,则y![]() ,所以点E(0,
,所以点E(0,![]() ),所以kEA
),所以kEA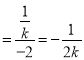 ,
,
所以直线EA:x=﹣2ky+2,联立与椭圆的方程整理得:∴y![]() ,x
,x![]() ,所以点G(
,所以点G(![]() ,
,![]() );
);
联立直线AM与椭圆的方程整理得:(1+2k2)x2﹣8k2x+8k2﹣4=0,解得:x1=2,x2![]() ,∴y2
,∴y2![]() ,所以点M(
,所以点M(![]() ,
,![]() ),
),
所以点M,G关于原点对称,即直线MG过原点,
∴S△AMG![]() 2|yM|
2|yM|![]() ,由题意得:
,由题意得:![]() 2
2![]() ,解得:k
,解得:k![]() ,
,
由点M(s,t)(t>0)得,k![]() ,所以直线AM为:y
,所以直线AM为:y![]() (x﹣2),
(x﹣2),
即直线AM:x![]() y﹣2=0.
y﹣2=0.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,EF![]() AB,平面BCF⊥平面ABCD,BF=CF,G为BC的中点,求证:
AB,平面BCF⊥平面ABCD,BF=CF,G为BC的中点,求证:

(1)OG∥平面ABFE;
(2)AC⊥平面BDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数h(x)是定义在(﹣2,2)上,满足h(﹣x)=﹣h(x),且x∈(0,2)时,h(x)=﹣2x,当x∈(﹣2,0)时,不等式[h(x)+2]2>h(x)m﹣1恒成立,则实数m的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() ),其中离心率
),其中离心率![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 为椭圆的左右焦点,若
为椭圆的左右焦点,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 的上顶点,若
的上顶点,若![]() ,试问直线
,试问直线![]() 是否经过定点,若经过定点,求出定点坐标,否则说明理由.
是否经过定点,若经过定点,求出定点坐标,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体ABCDEF满足:正方形ABCD与正三角形FBC所在的两个平面互相垂直,FB∥AE且FB=2EA.
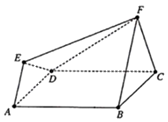
(1)证明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是R上的偶函数,对于
是R上的偶函数,对于![]() 都有
都有![]() 成立,且
成立,且![]() ,当
,当![]() ,且
,且![]() 时,都有
时,都有![]() .则给出下列命题:
.则给出下列命题:
①![]() ;
;
②函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ;
;
③函数![]() 在[﹣9,﹣6]上为减函数;④方程
在[﹣9,﹣6]上为减函数;④方程![]() 在[﹣9,9]上有4个根;
在[﹣9,9]上有4个根;
其中正确的命题序号是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函数f(x)的定义域;
(2)讨论函数f(x)的奇偶性;
(3)求a的取值范围,使f(x)>0在定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若不等式
,若不等式![]() 对一切
对一切![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(3)设数列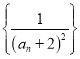 的前n项和为
的前n项和为![]() ,求证:对任意正整数n,都有
,求证:对任意正整数n,都有![]() 成立.
成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com