
【题目】将编号为1,2,…,18的18名乒乓球运动员分配在9张球台上进行单打比赛,规定每一张球台上两选手编号之和均为大于4的平方数.记{7号与18号比赛}为事件p.则p为( ).
A. 不可能事件 B. 概率为![]() 的随机事件
的随机事件
C. 概率为![]() 的随机事件 D. 必然事件
的随机事件 D. 必然事件
【答案】D
【解析】
由于编号最大的两数之和为![]() ,所以,同一张球台上两选手编号之和只能取3个平方数:25、16、9.现设同一张球台上两选手编号和为25、16、9的分别有x、y、z(x、y、z均为非负整数)个.依题意有
,所以,同一张球台上两选手编号之和只能取3个平方数:25、16、9.现设同一张球台上两选手编号和为25、16、9的分别有x、y、z(x、y、z均为非负整数)个.依题意有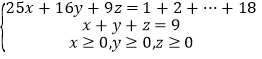 ,即
,即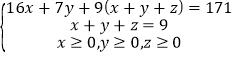 .得
.得![]() .
.
又由![]() ,知x只能取非负整数0,1,2,3,4,5.逐一代入检验,可得方程唯一的非负整数解
,知x只能取非负整数0,1,2,3,4,5.逐一代入检验,可得方程唯一的非负整数解![]() ,
,![]() ,
,![]() .
.
下面讨论9张球台上的选手对阵情况.
(1)由x=3,知平方数为25只能有3个,而编号不小于16的3个选手18,17,16对应的平方数又只能为25,故“两选手编号和为25”的只能是:18与7对阵,17与8对阵,16与9对阵.
(2)由![]() ,知去掉18,17,16,9,8,7后剩下的12个选手对应的平方数能且只能为16,有:1与15对阵,2与14对阵,3与13对阵,4与12对阵,5与11对阵,6与10对阵.
,知去掉18,17,16,9,8,7后剩下的12个选手对应的平方数能且只能为16,有:1与15对阵,2与14对阵,3与13对阵,4与12对阵,5与11对阵,6与10对阵.
所以,规定能够实现,且实现方案是唯一的.9张球台上选手对阵情况为:![]() .
.
事件p为必然事件.选D.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】为了研究经常使用手机是否对数学学习成绩有影响,某校高二数学研究性学习小组进行了调查,随机抽取高二年级50名学生的一次数学单元测试成绩,并制成下面的2×2列联表:
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 5 | 25 |
经常使用手机 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则有( )的把握认为经常使用手机对数学学习成绩有影响.
参考公式: ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.97.5%B.99%C.99.5%D.99.9%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①函数![]() 的最大值为1;
的最大值为1;
②已知集合![]() ,则集合A的真子集个数为3;
,则集合A的真子集个数为3;
③若![]() 为锐角三角形,则有
为锐角三角形,则有![]() ;
;
④“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 内单调递增”的充分必要条件.
内单调递增”的充分必要条件.
其中正确的命题是______.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() .
.
(1)若抛物线![]() 的焦点与
的焦点与![]() 的焦点重合,求
的焦点重合,求![]() 的标准方程;
的标准方程;
(2)若![]() 的上顶点
的上顶点![]() 、右焦点
、右焦点![]() 及
及![]() 轴上一点
轴上一点![]() 构成直角三角形,求点
构成直角三角形,求点![]() 的坐标;
的坐标;
(3)若![]() 为
为![]() 的中心,
的中心,![]() 为
为![]() 上一点(非
上一点(非![]() 的顶点),过
的顶点),过![]() 的左顶点
的左顶点![]() ,作
,作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色、相邻区域颜色不同,则区域不同涂色的方法种数为( )
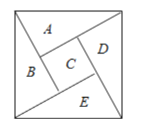
A.360B.400C.420D.480
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试问:能否把2008表示成![]() 的形式?如果可以,这种表示方式是否有无限多个?其中,m、n均为大于100且小于170的正整数,且
的形式?如果可以,这种表示方式是否有无限多个?其中,m、n均为大于100且小于170的正整数,且![]() ;
;![]() 均为两两不相等的小于6的正有理数,且
均为两两不相等的小于6的正有理数,且![]() 均为大于1且小于5的正整数,同时,
均为大于1且小于5的正整数,同时, ![]() 两两不相等,
两两不相等,![]() 也两两不相等请说明理由.
也两两不相等请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com