
 解:采用椭圆旋转而成的曲面,
解:采用椭圆旋转而成的曲面, +
+ =1,
=1, (p+
(p+ )=
)= (2.8+
(2.8+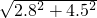 )≈4.05cm,b=
)≈4.05cm,b=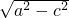 ≈3.37m.
≈3.37m. +
+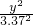 =1.
=1.

科目:高中数学 来源: 题型:填空题
 的定义域是(0,+∞);
的定义域是(0,+∞);查看答案和解析>>
科目:高中数学 来源: 题型:解答题
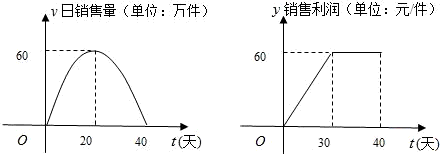 某公司是专门生产健身产品的企业,第一批产品A上市销售40天内全部售完,该公司对第一批产品A上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品A的销售利润与上市时间的关系.
某公司是专门生产健身产品的企业,第一批产品A上市销售40天内全部售完,该公司对第一批产品A上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品A的销售利润与上市时间的关系.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
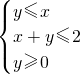 则目标函数z=2x+y的最大值为________;在平面直角坐标系中,该约束条件所表示的平面区域的面积为________.
则目标函数z=2x+y的最大值为________;在平面直角坐标系中,该约束条件所表示的平面区域的面积为________.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 ),给出四个命题:①它的周期是π;②它的图象关于直线x=
),给出四个命题:①它的周期是π;②它的图象关于直线x= 成轴对称;③它的图象关于点(
成轴对称;③它的图象关于点( ,0)成中心对称;④它在区间[-
,0)成中心对称;④它在区间[- ,
, ]上是增函数.其中正确命题的序号是 ________.
]上是增函数.其中正确命题的序号是 ________.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,求此时a的值.
,求此时a的值. ,求此时a的值.
,求此时a的值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com