
����Ŀ��ij���мƻ����¶���һ�����̣�ÿ���������ͬ�������ɱ�ÿƿ4Ԫ���ۼ�ÿƿ6Ԫ��δ�۳������̽��۴�������ÿƿ2Ԫ�ļ۸���ȫ�������꣮�����������۾��飬ÿ���������뵱��������£���λ���棩�йأ����������²�����25��������Ϊ500ƿ������������λ������[20��25����������Ϊ300ƿ�����������µ���20��������Ϊ200ƿ��Ϊ��ȷ�����·ݵĶ����ƻ���ͳ����ǰ�������·ݸ��������������ݣ��������Ƶ���ֲ�����
������� | [10��15�� | [15��20�� | [20��25�� | [25��30�� | [30��35�� | [35��40�� |
���� | 2 | 16 | 36 | 25 | 7 | 4 |
���������λ�ڸ������Ƶ�ʴ����������λ�ڸ�����ĸ��ʣ�
���������·���������һ���������X����λ��ƿ���ķֲ��У�
���������·�һ�������������̵�����ΪY����λ��Ԫ���������·���������һ��Ľ�����n����λ��ƿ��Ϊ����ʱ��Y����ѧ�����ﵽ���ֵ��
���𰸡��⣺����������֪X�Ŀ���ȡֵΪ200��300��500��
P��X=200��= ![]() =0.2��
=0.2��
P��X=300��= ![]() ��
��
P��X=500��= ![]() =0.4��
=0.4��
��X�ķֲ���Ϊ��
X | 200 | 300 | 500 |
P | 0.2 | 0.4 | 0.4 |
����n��200ʱ��Y=n��6��4��=2n��400��EY��400��
��200��n��300ʱ��
��x=200����Y=200����6��4��+��n��200����2��4��=800��2n��
��x��300����Y=n��6��4��=2n��
��EY=p��x=200������800��2n��+p��x��300����2n=0.2��800��2n��+0.8=1.2n+160��
��EY��1.2��300+160=520��
��300��n��500ʱ����x=200����Y=800��2n��
��x=300����Y=300����6��4��+��n��300������2��4��=1200��2n��
�൱n=300ʱ����EY��max=640��0.4��300=520��
��x=500����Y=2n��
��EY=0.2����800��2n��+0.4��1200��2n��+0.4��2n=640��0.4n��
��n��500ʱ��Y=  ��
��
EY=0.2��800��2n��+0.4��1200��2n��+0.4��2000��2n��=1440��2n��
��EY��1440��2��500=440��
���ϣ���n=300ʱ��EY���ֵΪ520Ԫ��
������������������֪X�Ŀ���ȡֵΪ200��300��500���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��У�
����n��200ʱ��Y=n��6��4��=2n��400��EY��400����200��n��300ʱ��EY��1.2��300+160=520����300��n��500ʱ��n=300ʱ����EY��max=640��0.4��300=520����n��500ʱ��EY��1440��2��500=440���Ӷ��õ���n=300ʱ��EY���ֵΪ520Ԫ��
�����㾫�����������⣬������Ҫ�˽���ɢ�������������ֲ���(���������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ���)��


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��У�����̻����������������ִ�����2�꣬�������ijɻ���Ϊ![]() ���ijɻ���Ϊ
���ijɻ���Ϊ![]() ������ÿ�����ɻ�������������.��
������ÿ�����ɻ�������������.��
�������������ɻ�һ��ĸ��ʣ�
����������ʾ�������ɻ���������������ķֲ��м���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͷijͨѶ�豸��Ϊ��Ӧ�г�����,���Ч��,��Ͷ��98��Ԫ���������Ƚ��豸����6��,������Ͷ������.��һ����Ҫ�ĸ��ַ�����12��Ԫ,�ӵڶ��꿪ʼ,������û����һ������4��Ԫ,��ÿ����������豸�ɻ�õ�������Ϊ50��Ԫ.
���������������,����������⣺(1)�������豸�������,�ջسɱ�����ʼӯ����(2)�������豸�������,�����ִ�����������һ�֣���ƽ��ӯ���ﵽ���ֵʱ,��26��Ԫ�ļ۸��������ڶ��֣�ӯ���ܶ�ﵽ���ֵʱ,��8��Ԫ�ļ۸�����.�����ַ�����Ϊ���㣿��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Σ����ij��˾�ij��ڶ��½���Ϊ���й�ר��������ִٽ����ڵķ�����ÿ�ַ�������Ҫ������ʵʩ����ʵʩ����һ��Ԥ�Ƶ�һ�����ʹ���ڶ�ָ���Σ��ǰ��![]() ����
����![]() ����
����![]() ���ĸ��ʷֱ�Ϊ
���ĸ��ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ���ڶ������ʹ���ڶ�Ϊ��һ���
���ڶ������ʹ���ڶ�Ϊ��һ���![]() ����
����![]() ���ĸ��ʷֱ�Ϊ
���ĸ��ʷֱ�Ϊ![]() ��
��![]() ����ʵʩ��������Ԥ�Ƶ�һ�����ʹ���ڶ�ָ���Σ��ǰ��
����ʵʩ��������Ԥ�Ƶ�һ�����ʹ���ڶ�ָ���Σ��ǰ��![]() ����
����![]() ����
����![]() ���ĸ��ʷֱ�Ϊ
���ĸ��ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ���ڶ������ʹ���ڶ�Ϊ��һ���
���ڶ������ʹ���ڶ�Ϊ��һ���![]() ����
����![]() ���ĸ��ʷֱ�Ϊ
���ĸ��ʷֱ�Ϊ![]() ��
��![]() ��ʵʩÿ�ַ�����һ����ڶ������������
��ʵʩÿ�ַ�����һ����ڶ������������![]() ��ʾ����
��ʾ����![]() ʵʩ�������ڶ�ﵽΣ��ǰ�ı�����
ʵʩ�������ڶ�ﵽΣ��ǰ�ı�����
��1��д��![]() �ķֲ��У�
�ķֲ��У�
��2��ʵʩ���ַ������������ڶ��Σ��ǰ���ڶ�ĸ��ʸ���
��3���������ַ��������ʵʩ�������ڶ�ﲻ����ǡ�ôﵽ������Σ��ǰ���ڶԤ������ֱ�Ϊ![]() ��Ԫ��
��Ԫ��![]() ��Ԫ��
��Ԫ��![]() ��Ԫ����ʵʩ���ַ�����ƽ���������
��Ԫ����ʵʩ���ַ�����ƽ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԭ��Ķ�ֱ��l��Բ![]() �ཻ�ڲ�ͬ������A��B��
�ཻ�ڲ�ͬ������A��B��
��1�����߶�AB���е�M�Ĺ켣C�ķ��̣�
��2���Ƿ����ʵ��k��ʹ��ֱ��L��y=k��x��4��������Cֻ��һ�����㣿�����ڣ����k��ȡֵ��Χ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)��ln x��a(x��1)��g(x)��ex.
(1)����f(x)�ĵ������䣻
(2)������h(x)��f(x��1)��g(x)����x>0ʱ��h(x)>1���������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪0��a��b����a+b=1�������в���ʽ����ȷ���ǣ� ��
A.log2a��0
B.2a��b�� ![]()
C.log2a+log2b����2
D.2�� ![]() +
+ ![]() ����
���� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±������ʮ����˻����ݡ������������Լ���������Ͻ��õĽ�����������
��õĽ�������ͳ�����ݣ�
��� | 1972 | 1976 | 1980 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
��� | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
������� | ���� �¹� | ���ô� | ���� | ���� | ���� | ������ | ���� | �Ĵ� ���� | ϣ�� | �й� |
�Ͻ������ | 5 | 0 | 49 | δ�μ� | 6 | 1 | 37 | 9 | 4 | 32 |
��������� | 13 | 0 | 80 | 83 | 12 | 13 | 44 | 16 | 6 | 51 |
ij����������֯�������ϱ��о������������������˻�֮��Ĺ�ϵ��
��1�������������Ͻ��������������Ϊ![]() �����ڵ����������������Ϊ
�����ڵ����������������Ϊ![]() ��֮������Իع鷽��
��֮������Իع鷽��
![]() ����
����![]()
��2����2008���29�챱�����˻����ձ����9����ƣ���ݴ����Իع鷽�̹�����2020 ��� 32 �춫
�����˻����ձ�����õĽ�����Ϊ�����н�������ȷ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��
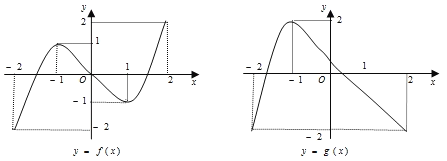
���������ĸ����⣺
(1)����![]() ���ҽ���6������
���ҽ���6������
(2)����![]() ���ҽ���3������
���ҽ���3������
(3)����![]() ���ҽ���5������
���ҽ���5������
(4)����![]() ���ҽ���4������
���ҽ���4������
������ȷ����ĸ�����( )
A. 4��B. 3��C. 2��D. 1��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com