练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．计算
    （1）log225•log34•log59        
    （2）$\frac{1}{2}$lg$\frac{32}{49}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{245}$．

    分析 利用对数运算法则求解即可．

    解答 解：（1）log225•log34•log59=8log25•log32•log53=8．
    （2）$\frac{1}{2}$lg$\frac{32}{49}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{245}$=$\frac{5}{2}$lg2-lg7-2lg2+$\frac{1}{2}$（lg5+2lg7）=$\frac{1}{2}$（lg2+lg5）=$\frac{1}{2}$．

    点评 本题考查对数运算法则的应用，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．已知正项数列{an}满足：a1=1，an2+2a2n+1≤3anan+1．
    （1）求证：$\frac{1}{{2}^{n-1}}$≤an≤1．
    （2）设bn=$\frac{{a}_{n}}{{{a}^{2}}_{n+1}}$-$\frac{1}{{a}_{n+1}}$，求证：b1+b2+b3+…+bn＜2n+1-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．设f（x）=2sin（ωx），其中ω＞0，若函数f（x）在区间[-$\frac{π}{4}$，$\frac{2π}{3}$]上是增函数，则ω的取值范围是（0，$\frac{3}{4}$ ）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．如图所示，在正方形纸片ABCD中，AC与BD相交于点O，剪去△AOB，将剩余部分沿OC、OD折叠，使OA、OB重合，则在以A（B）、C、D、O为顶点的四面体中，二面角O-AD-C的余弦值为（　　）
    A．$\frac{\sqrt{6}}{5}$B．$\frac{\sqrt{3}}{3}$C．$\frac{\sqrt{5}}{3}$D．$\frac{\sqrt{6}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

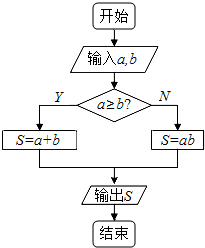    8．定义一种运算S=a?b，在如图所示的框图所表达的算法中揭示了这种运算“?”的含义，那么按照运算“?”的含义，S=tan60°?tan30°+cos60°?cos30°=（　　）
    A．$\frac{{3+\sqrt{3}}}{2}$B．$\frac{{4+\sqrt{3}}}{4}$C．$\frac{{19\sqrt{3}}}{12}$D．$\frac{{11\sqrt{3}}}{6}+\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知?x∈（0，+∞），[（m-1）x-1]（x2-mx-1）≥0恒成立，则m的值为$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知一个正方体的所有棱与空间的某一平面成角为α，则cosα的值为（　　）
    A．$\frac{\sqrt{3}}{3}$B．$\frac{\sqrt{6}}{3}$C．$\frac{\sqrt{2}}{2}$D．$\frac{\sqrt{3}}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

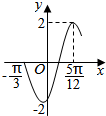
    2．函数f（x）=2sin（ωx+φ）（ω＞0，一$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则（　　）
    A．函数f（x）的最小正周期是2π
    B．函数f（x）的图象可由函数g（x）=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到
    C．函数f（x）的图象关于直线x=一$\frac{π}{12}$对称
    D．函数f（x）在区间[-$\frac{7π}{12}$+kπ，-$\frac{π}{12}$+kπ]（k∈Z）上是增函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数$f（x）=1+a•\frac{1}{2^x}+\frac{1}{4^x}$．
    （1）当a=1时，求函数f（x）在（-∞，0）上的值域；
    （2）若对任意x∈[0，+∞），总有f（x）＜3成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案