练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设 其中.

    (1)求的取值范围；

    (2)若，，求的值.

    （本小题满分12分）

    解：   ……2分

    （1）

    ……4分

     ∵  ∴即的取值范围是(0,2) ……6分

    （2）

           …………………..10分

          

                  

           因为所以    

           故………………………..12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=2lnx，g（x）=
    1
    2
    ax2+3x．
    （1）设直线x=1与曲线y=f（x）和y=g（x）分别相交于点P、Q，且曲线y=f（x）和y=g（x）在点P、Q处的切线平行，若方程
    1
    2
    f（x2+1）+g（x）=3x+k有四个不同的实根，求实数k的取值范围；
    （2）设函数F（x）满足F（x）+x[f′（x）-g′（x）]=-3x2-（a+6）x+1．其中f′（x），g′（x）分别是函数f（x）与g（x）的导函数；试问是否存在实数a，使得当x∈（0，1]时，F（x）取得最大值，若存在，求出a的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•重庆模拟）2011年3月11日日本发生9.0级地震后，某国派遣了由9名医护人员和27名搜救人员组成的救援队到日本救援，谁知日本福岛核电站连续爆炸，使该救援队
    2
    3
    的医护人员和
    1
    3
    的搜救人员遭轻微核辐射．
    （Ⅰ）在该救援队中随机抽查3名救援队员，求恰有1名遭轻微核辐射的医护人员且至多1名遭轻微核辐射的搜救人员的概率；
    （Ⅱ）在该救援队中随机抽查3名医护人员，设其中遭轻微核辐射的人数为随机变量ξ，求ξ的分布列及数学期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源：安徽省两地三校2010-2011学年高一上学期期末联考数学试题 题型：044

    设其中．

    (1)求的取值范围；

    (2)若，，求的值．

    查看答案和解析>>

    科目：高中数学 来源：黄冈中学　高二数学(下册)、考试卷1　排列、组合和二项式定理同步 题型：044

    设(其中)．

    (1)若a=1，b=－3，c=0，且，求n的值；

    (2)已知a>0、c>0，对(1)中求的n有，且a－b＋c=0，求ac的最大值和对应的的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=x3-xn2++且存在x0∈(0,),使f(x0)=x0.

    (1)证明f(x)是R上的单调增函数;

    设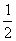

    其中,n=1,2,….

    (2)证明xn＜xn+1＜x0＜yn+1＜yn;

    (3)证明.

    查看答案和解析>>

    同步练习册答案