
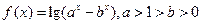
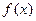 的定义域;
的定义域;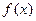 的图象上是否存在不同的两点,使过这两点的直线平行于
的图象上是否存在不同的两点,使过这两点的直线平行于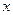 轴;
轴;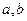 满足什么条件时,
满足什么条件时,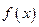 在
在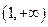 上恒取正值.
上恒取正值. 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源:不详 题型:解答题
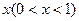 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为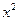 ,记改进工艺后,该公司销售纪念品的月平均利润是y(元)。
,记改进工艺后,该公司销售纪念品的月平均利润是y(元)。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
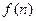 表示前
表示前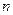 年的纯利润总和,
年的纯利润总和, 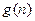 表示前
表示前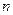 年的总支出.
年的总支出. 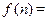 前
前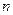 年的总收入-前
年的总收入-前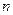 年的总支出-投资额].
年的总支出-投资额].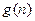 的关系式
的关系式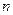 年的纯利润总和
年的纯利润总和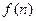 关于
关于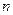 的函数关系式;并求该厂从第几年开始盈利?
的函数关系式;并求该厂从第几年开始盈利?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
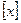 表示不超过
表示不超过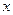 的最大整数,如
的最大整数,如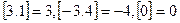 ,设函数
,设函数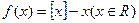 关于函数
关于函数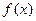 有如下四个命题:①
有如下四个命题:①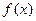 的值域为
的值域为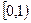 ②
②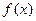 是偶函数 ③
是偶函数 ③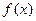 是周期函数,最小正周期为1 ④
是周期函数,最小正周期为1 ④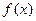 是增函数。
是增函数。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com