
【题目】如图,在正方体ABCD﹣A1B1C1D1中, 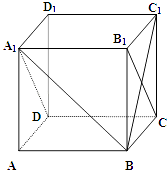
(1)证明:BC1⊥面A1B1CD;
(2)求直线A1B和平面A1B1CD所成的角.
【答案】
(1)解:连接B1C交BC1于点O,连接A1O.
在正方体ABCD﹣A1B1C1D1中
因为A1B1⊥平面BCC1B1.
所以A1B1⊥BC1.
又∵BC1⊥B1C,又BC1∩B1C=O
∴BC1⊥平面A1B1CD

(2)解:因为BC1⊥平面A1B1CD,所以A1O为斜线A1B在平面A1B1CD内的射影,所以∠BA1O为A1B与平面A1B1CD所成的角.设正方体的棱长为a
在RT△A1BO中,A1B= ![]() a,BO=
a,BO= ![]() a,所以BO=
a,所以BO= ![]() A1B,∠BA1O=30°,
A1B,∠BA1O=30°,
即直线A1B和平面A1B1CD所成的角为30°
【解析】(1)要证BC1⊥面A1B1CD;应通过证明A1B1⊥BC1 . BC1⊥B1C两个关系来实现,两关系容易证明.(2)因为BC1⊥平面A1B1CD,所以A1O为斜线A1B在平面A1B1CD内的射影,所以∠BA1O为A1B与平面A1B1CD所成的角.在RT△A1BO中求解即可.
【考点精析】关于本题考查的直线与平面垂直的判定和空间角的异面直线所成的角,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则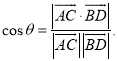 才能得出正确答案.
才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=xsinx,x1、x2∈[﹣ ![]() ,
, ![]() ],且f(x1)>f(x2),则下列结论必成立的是( )
],且f(x1)>f(x2),则下列结论必成立的是( )
A.x1>x2
B.x1+x2>0
C.x1<x2
D.x12>x22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称,当函数
轴对称,当函数![]() 和
和![]() 在区间
在区间![]() 同时递增或同时递减时,把区间
同时递增或同时递减时,把区间![]() 叫做函数
叫做函数![]() 的“不动区间”.若区间
的“不动区间”.若区间![]() 为函数
为函数![]() 的“不动区间”,则实数
的“不动区间”,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() )的图象如图所示,直线x=
)的图象如图所示,直线x= ![]() ,x=
,x= ![]() 是其两条对称轴.
是其两条对称轴. 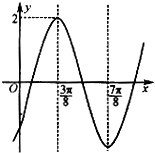
(1)求函数f(x)的解析式及单调区间;
(2)若f(α)= ![]() ,且
,且 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时, ![]() (
(![]() ),且曲线
),且曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)求![]() 的值及函数
的值及函数![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上有三个零点,求实数
上有三个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的方程为:ax2+ay2﹣2a2x﹣4y=0(a≠0,a为常数).
(1)判断曲线C的形状;
(2)设曲线C分别与x轴、y轴交于点A、B(A、B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;
(3)设直线l:y=﹣2x+4与曲线C交于不同的两点M、N,且|OM|=|ON|,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求证: ![]() 与
与 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 与
与 ![]() ﹣k
﹣k ![]() 的长度相等,求β﹣α的值(k为非零的常数).
的长度相等,求β﹣α的值(k为非零的常数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com