练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设、分别是椭圆：的左右焦点。

    （Ⅰ）设椭圆上的点到两点、距离之和等于，写出椭圆的方程和焦点坐标；

    （Ⅱ）设是（1）中所得椭圆上的动点，求线段的中点的轨迹方程；

    (Ⅲ）设点是椭圆上的任意一点，过原点的直线与椭圆相交于，两点，当直线 ， 的斜率都存在，并记为， ，试探究的值是否与点及直线有关，不必证明你的结论。

    （Ⅰ）椭圆C的方程为  

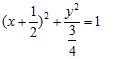    （Ⅱ） (Ⅲ）的值与点P的位置无关，同时与直线L无关


    解析:

    （Ⅰ）由于点在椭圆上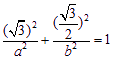， ……………………… 1分

    2=4,                                            ………………………2分  

    椭圆C的方程为                        ………………………3分

    焦点坐标分别为               ………………………4分

    （Ⅱ）设的中点为B（x, y）则点 ………………………5分

    把K的坐标代入椭圆中得………7分

    线段的中点B的轨迹方程为 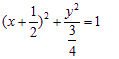  ………………8分

    （Ⅲ）过原点的直线L与椭圆相交的两点M，N关于坐标原点对称 

    设                  

    在椭圆上，应满足椭圆方程，得  ……10分

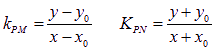              ………………11分

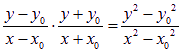    ==       ………………13分

    故：的值与点P的位置无关，同时与直线L无关，………………14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•徐州一模）如图，在平面直角坐标系xOy中，椭圆E：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的焦距为2，且过点(
    		2
    ，
    		6
    2
    )    ．
    （1）求椭圆E的方程；
    （2）若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M．
    （ⅰ）设直线OM的斜率为k1，直线BP的斜率为k2，求证：k1k2为定值；
    （ⅱ）设过点M垂直于PB的直线为m．求证：直线m过定点，并求出定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，已知椭圆E：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）的离心率为
    1
    2
    ，一条准线方程为x=4．
    （1）求椭圆E的标准方程；
    （2）若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M，设直线OM的斜率为k1，直线BP的斜率为k2，求证：k1k2为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点P（-1，
    3
    2
    ）是椭圆E：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）上一点，F1、F2分别是椭圆E的左、右焦点，O是坐标原点，PF1⊥x轴．
    （1）求椭圆E的方程；
    （2）设A、B是椭圆E上两个动点，
    PA
    +
    PB
    =λ
    PO
    （0＜λ＜4，且λ≠2）．求证：直线AB的斜率等于椭圆E的离心率；
    （3）在（2）的条件下，当△PAB面积取得最大值时，求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点P（-1，
    3
    2
    ）是椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）上一点F1、F2分别是椭圆C的左、右焦点，O是坐标原点，PF1⊥x轴．
    ①求椭圆C的方程；
    ②设A、B是椭圆C上两个动点，满足：
    PA
    +
    PB
    =λ
    PO
    （0＜λ＜4，且λ≠2）求直线AB的斜率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•安徽）设椭圆E：
    x2
    a2
    +
    y2
    1-a2
    =1    的焦点在x轴上
    （1）若椭圆E的焦距为1，求椭圆E的方程；
    （2）设F1，F2分别是椭圆E的左、右焦点，P为椭圆E上第一象限内的点，直线F2P交y轴于点Q，并且F1P⊥F1Q，证明：当a变化时，点P在某定直线上．

    查看答案和解析>>

    同步练习册答案