
【题目】如图,四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的动点.
上的动点.
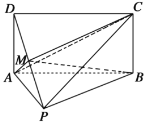
(1)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积记为
的体积记为![]() ,四棱锥
,四棱锥![]() 的体积记为
的体积记为![]() ,当
,当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接![]() ,
,![]() ,记它们的交点为
,记它们的交点为![]() ,连接
,连接![]() ,利用中位线可得
,利用中位线可得![]() ,再利用线面平行的判定定理可证.
,再利用线面平行的判定定理可证.
(2)设![]() ,取
,取![]() 中点
中点![]() ,利用三棱锥的体积公式和
,利用三棱锥的体积公式和![]() ,可得
,可得![]() ,再建立空间直角坐标系,利用向量可得二面角
,再建立空间直角坐标系,利用向量可得二面角![]() 的余弦值.
的余弦值.
(1)连接![]() ,
,![]() ,记它们的交点为
,记它们的交点为![]() ,连接
,连接![]()
因为四边形![]() 为矩形,∴
为矩形,∴![]() 为
为![]() 中点,
中点,
又![]() 为线段
为线段![]() 的中点,∴
的中点,∴![]() ,
,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() .
.
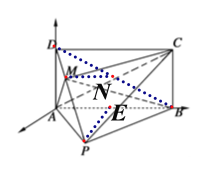
(2)∵矩形![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
设![]() ,取
,取![]() 中点
中点![]() ,
,
因为![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
又因为![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,且
,且![]() ,
,
设三棱锥![]() 的高为
的高为![]() ,则
,则![]() ,∴
,∴![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() ,
,
由题意,如图以![]() 点为坐标原点建立空间直角坐标系,则
点为坐标原点建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]()
∵![]() ,∴
,∴![]() ,
,
易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则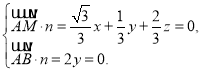
令![]() 则得平面
则得平面![]() 的一个法向量
的一个法向量![]() ,
,
![]()
因为二面角![]() 为锐角二面角,
为锐角二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
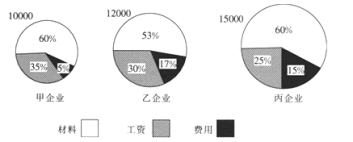
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的首项
的首项![]() 及数列的递推关系式
及数列的递推关系式![]() ;
;
(2)若数列![]() 成等比数列,求常数
成等比数列,求常数![]() 的值,并求数列
的值,并求数列![]() 的通项公式;
的通项公式;
(3)数列![]() 中是否存在三项
中是否存在三项![]() 、
、![]() 、
、![]() ,它们组成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
,它们组成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,SA⊥底面ABCD,底面ABCD是平行四边形,E是线段SD上一点.

(1)若E是SD的中点,求证:SB∥平面ACE;
(2)若SA=AB=AD=2,SC=2![]() ,且DE
,且DE![]() DS,求二面角S﹣AC﹣E的余弦值.
DS,求二面角S﹣AC﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】所谓声强,是指声音在传播途径上每1平方米面积上的声能流密度,用I表示,人类能听到的声强范围很广,其中能听见的1000Hz声音的声强(约10﹣12W/m2)为标准声强,记作I0,声强I与标准声强I0之比的常用对数称作声强的声强级,记作L,即L=lg![]() ,声强级L的单位名称为贝(尔),符号为B,取贝(尔)的十分之一作为响度的常用单位,称为分贝(尔).简称分贝(dB).《三国演义》中有张飞喝断当阳桥的故事,设张飞大喝一声的响度为140dB.一个士兵大喝一声的响度为90dB,如果一群士兵同时大喝一声相当一张飞大喝一声的响度,那么这群土兵的人数为( )
,声强级L的单位名称为贝(尔),符号为B,取贝(尔)的十分之一作为响度的常用单位,称为分贝(尔).简称分贝(dB).《三国演义》中有张飞喝断当阳桥的故事,设张飞大喝一声的响度为140dB.一个士兵大喝一声的响度为90dB,如果一群士兵同时大喝一声相当一张飞大喝一声的响度,那么这群土兵的人数为( )
A.1万B.2万C.5万D.10万
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 过点(0,1)且离心率
过点(0,1)且离心率![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设动直线l与两定直线l1:x﹣y=0和l2:x+y=0分别交于P,Q两点.若直线l总与椭圆E有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 为曲线
为曲线![]() 上的点,
上的点,![]() ,垂足为
,垂足为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为正整数,若两个项数都不小于
为正整数,若两个项数都不小于![]() 的数列
的数列![]() ,
,![]() 满足:存在正数
满足:存在正数![]() ,当
,当![]() 且
且![]() 时,都有
时,都有![]() ,则称数列
,则称数列![]() ,
,![]() 是“
是“![]() 接近的”.已知无穷等比数列
接近的”.已知无穷等比数列![]() 满足
满足![]() ,无穷数列
,无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 通项公式;
通项公式;
(2)求证:对任意正整数![]() ,数列
,数列![]() ,
,![]() 是“
是“![]() 接近的”;
接近的”;
(3)给定正整数![]() ,数列
,数列![]() ,
,![]() (其中
(其中![]() )是“
)是“![]() 接近的”,求
接近的”,求![]() 的最小值,并求出此时的
的最小值,并求出此时的![]() (均用
(均用![]() 表示).(参考数据:
表示).(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的通项公式为
的通项公式为![]() ,其中
,其中![]() ,
,![]() 、
、![]() .
.
(1)试写出一组![]() 、
、![]() 的值,使得数列
的值,使得数列![]() 中的各项均为正数.
中的各项均为正数.
(2)若![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,且对任意的
,且对任意的![]() (
(![]() ),均有
),均有![]() ,写出所有满足条件的
,写出所有满足条件的![]() 的值.
的值.
(3)若![]() ,数列
,数列![]() 满足
满足![]() ,其前
,其前![]() 项和为
项和为![]() ,且使
,且使![]() (
(![]() 、
、![]() ,
,![]() )的
)的![]() 和
和![]() 有且仅有
有且仅有![]() 组,
组,![]() 、
、![]() 、…、
、…、![]() 中有至少
中有至少![]() 个连续项的值相等,其它项的值均不相等,求
个连续项的值相等,其它项的值均不相等,求![]() 、
、![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com