
【题目】已知数列{an}是首项为a1=![]() ,公比q=
,公比q=![]() 的等比数列,设
的等比数列,设![]() ,数列
,数列![]() 满足cn=an·bn.
满足cn=an·bn.
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤![]() m2+m-1对一切正整数n恒成立,求实数m的取值范围.
m2+m-1对一切正整数n恒成立,求实数m的取值范围.
 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB平面PAD,△PAD是正三角形,DC//AB,DA=DC=2AB.
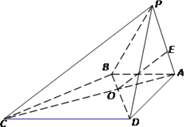
(1)若点E为棱PA上一点,且OE∥平面PBC,求![]() 的值;
的值;
(2)求证:平面PBC平面PDC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a、b、c分别为内角A、B、C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC
(1)求A的大小;
(2)若sinB+sinC=1,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若![]() ,求实数k的值;
,求实数k的值;
(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() +
+![]() =1的左、右焦点分别为F1,F2,一条直线
=1的左、右焦点分别为F1,F2,一条直线![]() 经过点F1与椭圆交于A,B两点.
经过点F1与椭圆交于A,B两点.
(1)求△ABF2的周长;
(2)若![]() 的倾斜角为
的倾斜角为![]() ,求弦长|AB|.
,求弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x不等式x2﹣2mx+m+2<0(m∈R)的解集为M.
(1)当M为空集时,求m的取值范围;
(2)在(1)的条件下,求![]() 的最大值;
的最大值;
(3)当M不为空集,且M![]() [1,4]时,求实数m的取值范围.
[1,4]时,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
|
|
|
|
|
|
|
|
|
|
(1)请画出上表数据的散点图;并指出![]() 是否线性相关;
是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
![]() ;
;
(3)已知该厂技术改造前![]() 吨甲产品能耗为
吨甲产品能耗为![]() 吨标准煤,试根据求出的线性回归方程,预测生产
吨标准煤,试根据求出的线性回归方程,预测生产![]() 吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,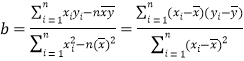 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱中![]() ,点P,G分别是AD,EF的中点,已知
,点P,G分别是AD,EF的中点,已知![]() 平面ABC,AD=EF=3,DE=DF=2.
平面ABC,AD=EF=3,DE=DF=2.
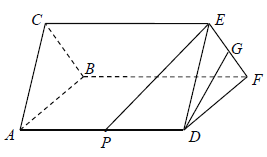
(Ⅰ)求证:DG⊥平面BCEF;
(Ⅱ)求PE与平面BCEF 所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com