
椭圆C的中心为原点, 右焦点F(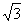 ,0), 以短轴的两端点及F为顶点的三角形恰为等边三角形.
,0), 以短轴的两端点及F为顶点的三角形恰为等边三角形.
(1)求椭圆C的标准方程;
(2)过椭圆C内的一点P(0,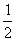 )作直线l交椭圆C于M、 N,求MN中点Q的轨迹方程;
)作直线l交椭圆C于M、 N,求MN中点Q的轨迹方程;
(3)在(2)条件下,求△OMN的面积最大值.
(1)设椭圆C的标准方程为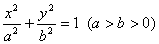 ,
,
∵ 右焦点为F(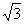 ,0) ∴
,0) ∴ 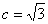
又∵ △B1FB2为正三角形 ∴ 
结合  得
得  ,
,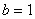
∴ 椭圆C的标准方程是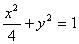 ………………………………… 4分
………………………………… 4分
(2)设Q(x,y),M(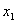 ,
, ),N(
),N( ,
,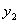 )
)
当直线l的斜率存在时,直线l的方程为
代入 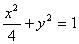 得
得 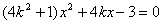
∴  ,
,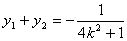 …………………… 6分
…………………… 6分
∴ 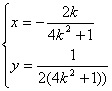
消去k得 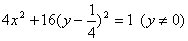 …………………………… 8分
…………………………… 8分
又∵ k不存在时,点Q为(0,0)也满足上述方程,
∴ 线段MN的中点Q的轨迹方程是  ……… 9分
……… 9分
(3)由(2)知,M(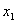 ,
, ),N(
),N( ,
,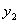 ),直线l的方程为
),直线l的方程为
代入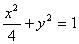 得
得 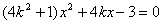
∴  ,
,
∴ 
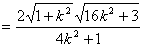 ………………………………………………… 11分
………………………………………………… 11分
又∵ 原点O到直线l的距离为
∴ 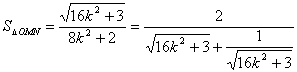 ……………… 12分
……………… 12分
设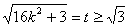
∴ 
∴ △OMN面积的最大值为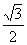 ……………………………………… 14分
……………………………………… 14分


科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| y2 |
| 16 |
| x2 |
| 2 |
| y2 |
| 16 |
| x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
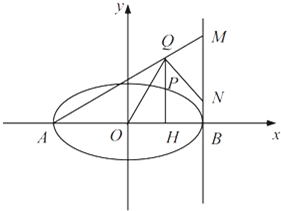 (2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
(2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
| ||
| 2 |
| ||
| 2 |
| PQ |
| HP |
| BM |
| BN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| 1 |
| 2 |
| PA |
| PB |
| PF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 8 |
| 2 |
| x2 |
| 2 |
| x2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com