
����Ŀ������������֯�������о�������ʾ��Ŀǰ�й����ӻ����������6�ڣ��������ʹ�ѧ���Ľ����ʾ��ѳ����߳ɣ�Ϊ���о�ÿ���ۼƻ��Ⱪ¶ʱ�䣨��λ��Сʱ������ӷ����ʵĹ�ϵ����ij��ѧһ�꼶200��ѧ�����в������ʾ����飬�õ��������ݣ�
ÿ���ۻ����Ⱪ¶ʱ�䣨��λ��Сʱ�� |
|
|
|
| ������28Сʱ |
�������� | 21 | 39 | 37 | 2 | 1 |
���������� | 3 | 37 | 52 | 5 | 3 |
��1����ÿ���ۼƻ��Ⱪ¶ʱ�䲻����28Сʱ��4��ѧ���У������ȡ2����������ǡ��һ��ѧ�������ӵĸ��ʣ�
��2����ÿ���ۼƻ��Ⱪ¶ʱ������14��Сʱ����֤Ϊ�����㹻�Ļ��Ⱪ¶ʱ�䡱����������������������������������ݣ�2���е��������ж��ܷ��ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ���㹻�Ļ��Ⱪ¶ʱ��������й�ϵ��
���� | ������ | |
�㹻�Ļ��Ⱪ¶ʱ�� | ||
���㹻�Ļ��Ⱪ¶ʱ�� |
��:![]()
P | 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
���𰸡�(1) ![]() (2)������
(2)������
��������
(1)�������⣬ʱ�䲻����28Сʱ��4��ѧ���У�����1����������3��������ǡ��һ�����ӣ�![]() ��4��ѧ����2�����У�
��4��ѧ����2�����У�![]() ��Ȼ����������.
��Ȼ����������.
(2)�ȸ��ݱ���ó��ڻ����ʱ������ӵ������ֱ��Ƕ��٣������������Ȼ����ݹ�ʽ���
![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() ���ó����.
�����.
��1���衰�����ȡ2��������ǡ��һ��ѧ�������ӡ�Ϊ�¼�![]() ����
����![]()
�������ȡ2��������ǡ��һ��ѧ�������ӵĸ���Ϊ![]() .
.
��2�������������ݵõ���������
���� | ������ | |
�㹻�Ļ��Ⱪ¶ʱ�� | 40 | 60 |
���㹻�Ļ��Ⱪ¶ʱ�� | 60 | 40 |
����![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() ��
��
�����ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ���㹻�Ļ��Ⱪ¶ʱ��������й�ϵ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ʵ�3��3�������Ϊ��T-����:
��1���������1���ĸ�����0��
��2�����С������Լ������Խ��߹���������������һ��������������������ȡ�
��ͬ��T-������________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����ǿѧ���ļ������ͱ�ʶ������֯��һ�����ơ���ǿ���ԡ���PK����![]() ���Ӹ���4��ѡ����ɣ�ÿ�����Ӹ���һ��ѡ��PK�������ľ�.��������ʤ�ߵ�2���⣬�������ʤ�߾���1�֣�ÿ�ֵĸ��ߵ�0��.����ÿ�ֱ���A��ѡ�ֻ�ʤ�ĸ��ʾ�Ϊ
���Ӹ���4��ѡ����ɣ�ÿ�����Ӹ���һ��ѡ��PK�������ľ�.��������ʤ�ߵ�2���⣬�������ʤ�߾���1�֣�ÿ�ֵĸ��ߵ�0��.����ÿ�ֱ���A��ѡ�ֻ�ʤ�ĸ��ʾ�Ϊ![]() ���Ҹ��ֱ���������������������ʱA�ӵĵ÷ָ���B�ӵĵ÷ֵĸ���Ϊ( )
���Ҹ��ֱ���������������������ʱA�ӵĵ÷ָ���B�ӵĵ÷ֵĸ���Ϊ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� 2022�걱�����»�����ɹ�����3�����ϱ�ѩ���ںŵ����������ѩ�������ĿѸ�ٳ�������������ij�ۺϴ�ѧ�ƻ���һ�꼶�������γ̣�Ϊ�˽�ѧ���Ա����˶�����Ȥ������Ӹ�Уһ�꼶ѧ���г�ȡ��100�˽��е��飬����Ů���жԱ����˶�����Ȥ��ռ![]() ����������10�˱�ʾ�Ա����˶�û����Ȥ��
����������10�˱�ʾ�Ա����˶�û����Ȥ��
��1����������![]() �����������ش��ܷ��ڷ�����ĸ��ʲ�����0.1��ǰ������Ϊ���Ա����Ƿ�����Ȥ���Ա��й�����
�����������ش��ܷ��ڷ�����ĸ��ʲ�����0.1��ǰ������Ϊ���Ա����Ƿ�����Ȥ���Ա��й�����
����Ȥ | û��Ȥ | �ϼ� | |
�� | 55 | ||
Ů | |||
�ϼ� |
��2������Ƶ����Ϊ���ʣ����ٴӸ�Уһ�꼶ȫ��ѧ���У�������������ķ���ÿ�γ�ȡ1��ѧ������ȡ5�Σ��DZ���ȡ��5��ѧ���жԱ�������Ȥ������Ϊ![]() ����ÿ�γ�ȡ�Ľ����������ģ���
����ÿ�γ�ȡ�Ľ����������ģ���![]() �ķֲ����������ͷ��
�ķֲ����������ͷ��
������
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072/p> | 2.706 | 3.841 | 5.024 | 6.635 |
�ο���ʽ��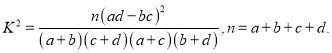
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����nΪһ������������ά�ռ��ڵĵ㼯S�����������ʣ�
��1��.�ռ��ڲ�����n��ƽ�棬ʹ�õ㼯S�е�ÿ������������n��ƽ���е�һ��ƽ���ϣ�
��2��.����ÿ����![]() ��������n��ƽ�棬ʹ��
��������n��ƽ�棬ʹ��![]() �е�ÿ�������������n��ƽ���е�һ��ƽ����.
�е�ÿ�������������n��ƽ���е�һ��ƽ����.
��㼯S�е�ĸ�������Сֵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����״������һ�����Ͳ������壬��֪�����ж������ۺ�����MERS�������ؼ��Ժ����ۺ�����SARS���Ƚ����صļ���������״������nCoV������ǰ��δ�������з��ֵĹ�״�����¶��꣬ijС��Ϊ��һ����������״������������֪ʶ�Ľ�������С���ڿ�չ������״�������߰�ȫ�����������ѧϰ���ڴ�֮����֯��������״�������߰�ȫ֪ʶ�������������֪��������ķֱ��Ǽס��ҡ���������λҵ������������λҵ����Ӧ������Ϊ��1��2��3��4������С��Ϊ�����ҵ���ǵIJ���Ⱥ����Ӷȣ�����С���ڵ�����ҵ���ڱ�������ǰ����λҵ�������ν���Ԥ�⣬��Ԥ����ȫ��ȷ��������Ʒ������a��b��c��d��ʾijҵ���Լס��ҡ���������λҵ������������һ�ֵȿ��ܵ�Ԥ�����У���X��|a��1|+|b��2|+|c��3|+|d��4|��
��1�����ҵ�������Ʒ�ĸ��ʣ�
��2����X�ķֲ��м���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() Ϊ��Բ
Ϊ��Բ![]() ���Ͻ��㣬
���Ͻ��㣬![]() ��һ��
��һ��![]() ��
��![]() ���Ϸ�����
���Ϸ�����![]() .
.
��1����ֱ��![]() �ķ��̣�
�ķ��̣�
��2��![]() Ϊֱ��
Ϊֱ��![]() ��
��![]() ����
����![]() �Ľ��㣬
�Ľ��㣬![]() ����
����![]() ��
��![]() ���е�ֱ�Ϊ
���е�ֱ�Ϊ![]() ����
����![]() ��ͬһֱ���ϣ���
��ͬһֱ���ϣ���![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)��![]() x2��lnx.
x2��lnx.
(1)����f(x)�ĵ������䣻
(2)��֤����x>1ʱ��![]() x2��lnx<
x2��lnx<![]() x3.
x3.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ�����¸�MN��ѡ��A����һ��ɽ�µ��¶�CΪ�����۲�㣮��A����M������ǡ�MAN=60����C������ǡ�CAB=45���Լ���MAC=75������C���á�MCA=60������֪�¸�BC=50�ף����¸�MN=______�ף�
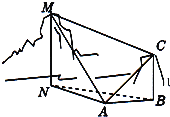
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com