
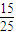 =0.6
=0.6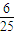 =0.24
=0.24

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
一个盒子中装有5个编号依次为1、2、3、4、5的球,这5个球除号码外完全相同,有放回的连续抽取两次,每次任意地取出一个球。
(1) 用列表或画树状图的方法列出所有可能结果。(4分)
(2) 求事件A=“取出球的号码之和不小于6”的概率。(5分)
(3)设第一次取出的球号码为x,第二次取出的球号码为y,求事件B=“点(x,y)落在直线 y = x+1 上方”的概率。 (5分)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年河南省南阳一中(下)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010年高考数学专项复习:概率与应用(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com