
【题目】已知 ![]() ,且
,且 ![]()
(1)当 ![]() 时,解不等式
时,解不等式 ![]() ;
;
(2)![]() 在
在 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:当 ![]() 时,解不等式
时,解不等式 ![]() ,得
,得 ![]() ,
,
即 ![]() ,
,
故不等式的解集为 ![]()
(2)解:由 ![]() 在
在 ![]() 恒成立,得
恒成立,得 ![]() 在
在 ![]() 恒成立,
恒成立,
①当 ![]() 时,有
时,有 ![]() ,得
,得 ![]() ,
,
②当 ![]() 时,有
时,有 ![]() ,得
,得 ![]() ,
,
故实数 ![]() 的取值范围
的取值范围 ![]()
【解析】(1)根据题意当m=2时可得到 3 < log2 x < 1利用对数的单调性可得出不等式的解集。(2)由f ( x ) < 0 在 [ 2 , 4 ] 恒成立得到 3 < logm x < 1 在 [ 2 , 4 ] 恒成立,分情况讨论分别解出m的取值范围然后并起来即可得到m的取值范围。
【考点精析】本题主要考查了对数的运算性质的相关知识点,需要掌握①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() 才能正确解答此题.
才能正确解答此题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy内,动点P到定点F(﹣1,0)的距离与P到定直线x=﹣4的距离之比为 ![]() .
.
(1)求动点P的轨迹C的方程;
(2)设点A、B是轨迹C上两个动点,直线OA、OB与轨迹C的另一交点分别为A1、B1 , 且直线OA、OB的斜率之积等于- ![]() ,问四边形ABA1B1的面积S是否为定值?请说明理由.
,问四边形ABA1B1的面积S是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】)已知命题p:“x∈[1,2],x2﹣a≥0”,命题q:“x∈R,x2+2ax+2﹣a=0”.若命题“p且q”是真命题,则实数a的取值范围为( )
A.﹣2≤a≤1
B.a≤﹣2或1≤a≤2
C.a≥1
D.a≤﹣2或 a=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( ) 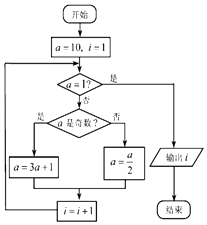
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x)满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[﹣8,8]上有四个不同的根x1 , x2 , x3 , x4 , 则x1+x2+x3+x4= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() 的左焦点为F1 , 右焦点为F2 , 过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1 , 右焦点为F2 , 过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形. 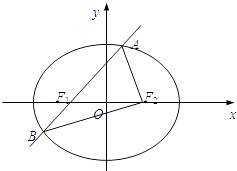
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:①以PQ为直径的圆与x轴的位置关系? ②在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一组数据如表:
x | 1 | 2 | 3 | 4 | 5 |
y | 1.3 | 1.9 | 2.5 | 2.7 | 3.6 |
(1)画出散点图;
(2)根据下面提供的参考公式,求出回归直线方程,并估计当x=8时,y的值.
(参考公式: ![]() =
=  =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com