
分析 (1)通过求导可知f′(x)=2•$\frac{c-{x}^{2}}{x}$,进而分c≤0与c>0两种情况讨论即可;
(2)通过求导、作差变形可知g′(ax1+bx2)=$\frac{2}{a{x}_{1}+b{x}_{2}}$-$\frac{2(ln{x}_{2}-ln{x}_{1})}{{x}_{2}-{x}_{1}}$+(2a-1)(x2-x1),利用分析法可知只需证明$\frac{2}{a{x}_{1}+b{x}_{2}}$-$\frac{2(ln{x}_{2}-ln{x}_{1})}{{x}_{2}-{x}_{1}}$<0,即要证$\frac{{x}_{2}-{x}_{1}}{a{x}_{1}+b{x}_{2}}$-ln$\frac{{x}_{2}}{{x}_{1}}$<0,进而换元、利用导数判断单调性即可.
解答 (1)解:由题可知x>0,f′(x)=2($\frac{c}{x}$-x)=2•$\frac{c-{x}^{2}}{x}$,
①若c≤0,则易知f′(x)<0,
∴f(x)在(0,+∞)上单调递减,故(0,+∞)为f(x)的单调递减区间;
②若c>0,令f′(x)=0可知x=$\sqrt{c}$,
且当x>$\sqrt{c}$时f′(x)<0,当0<x<$\sqrt{c}$时f′(x)>0,
∴f(x)的单调递减区间为($\sqrt{c}$,+∞),单调递增区间为(0,$\sqrt{c}$);
(2)证明:∵g(x)=f(x)-mx=2lnx-x2-mx,x>0,
∴g′(x)=$\frac{2}{x}$-2x-m,
又∵函数g(x)=f(x)-mx的图象与x轴交于A(x1,0),B(x2,0)两点,且0<x1<x2,
∴2lnx1-${x}_{1}^{2}$-mx1=0,2lnx2-${x}_{2}^{2}$-mx2=0,
两式相减,得m=$\frac{2(ln{x}_{2}-ln{x}_{1})}{{x}_{2}-{x}_{1}}$-(x1+x2),
∴g′(ax1+bx2)=$\frac{2}{a{x}_{1}+b{x}_{2}}$-2(ax1+bx2)-$\frac{2(ln{x}_{2}-ln{x}_{1})}{{x}_{2}-{x}_{1}}$+(x1+x2),
又∵a+b=1,
∴g′(ax1+bx2)=$\frac{2}{a{x}_{1}+b{x}_{2}}$-$\frac{2(ln{x}_{2}-ln{x}_{1})}{{x}_{2}-{x}_{1}}$+(2a-1)(x2-x1),
∵b≥a,2a≤1,
∴(2a-1)(x2-x1)≤0,
所以要证g'(ax1+bx2)<0,只需证$\frac{2}{a{x}_{1}+b{x}_{2}}$-$\frac{2(ln{x}_{2}-ln{x}_{1})}{{x}_{2}-{x}_{1}}$<0,
即要证$\frac{{x}_{2}-{x}_{1}}{a{x}_{1}+b{x}_{2}}$-ln$\frac{{x}_{2}}{{x}_{1}}$<0,
令$\frac{{x}_{2}}{{x}_{1}}$=t∈(1,+∞),即证$\frac{t-1}{a+bt}$-lnt<0,
记h(t)=$\frac{t-1}{a+bt}$-lnt,则h′(t)=$\frac{t-(a+bt)^{2}}{t(a+bt)^{2}}$,
又∵a+bt=1-b+bt=1+b(t-1)≥1+$\frac{1}{2}$(t-1)=$\frac{t+1}{2}$≥$\frac{2\sqrt{t}}{2}$=$\sqrt{t}$,
即(a+bt)2≥t,∴h′(t)=$\frac{t-(a+bt)^{2}}{t(a+bt)^{2}}$<0,
∴h(t)在(1,+∞)上单调递减,故h(t)<h(1)=0,即$\frac{t-1}{a+bt}$-lnt<0,
即$\frac{{x}_{2}-{x}_{1}}{a{x}_{1}+b{x}_{2}}$-ln$\frac{{x}_{2}}{{x}_{1}}$<0,故g'(ax1+bx2)<0.
点评 本题是一道关于函数的综合应用题,利用导数这个工具是解题的核心,考查分类讨论的思想,以及分析法来证明恒成立问题,注意解题方法的积累,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 空间中任意三点确定一个平面 | |
| B. | 直线上的两点和直线外的一点可以确定一个平面 | |
| C. | 分别在三条不同的直线上的三点确定一个平面 | |
| D. | 不共线的四点确定一个平面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{11}{3}$ | C. | $\frac{25}{6}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
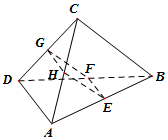 (文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,
(文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com