
 某小区规划一块周长为2a(a为正常数)的矩形停车场,其中如图所示的直角三角形ADP内为绿化区域.且∠PAC=∠CAB.设矩形的长AB=x,AB>AD
某小区规划一块周长为2a(a为正常数)的矩形停车场,其中如图所示的直角三角形ADP内为绿化区域.且∠PAC=∠CAB.设矩形的长AB=x,AB>AD| AD |
| DP |
| a |
| 2 |
| a-x |
| x |
| AD |
| DP |
| a-x |
| DP |
| 2ax-a2 |
| 2x |
| 2ax-a2 |
| 2x |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 4 |
| a2 |
| x |
| a2 |
| x |
| 2 |
| ||
| 2 |
| ||
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| AD |
| DP |
| 1 |
| 2 |
| a |
| 4 |
| a2 |
| x |


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
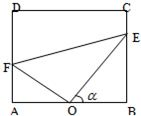 某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=25
某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=25| 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省无锡一中高一(下)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
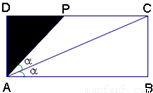
(14分)某小区规划一块周长为![]() (
(![]() 为正常数)的矩形停车场,其中如图所示的直角三角形
为正常数)的矩形停车场,其中如图所示的直角三角形![]() 内为绿化区域.且
内为绿化区域.且![]() .设矩形的长
.设矩形的长![]() ,
,![]()
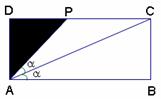 (1)求线段
(1)求线段![]() 的长关于
的长关于![]() 的函数
的函数![]() 表达式并指出定义域;
表达式并指出定义域;
(2)应如何规划矩形的长![]() ,使得绿化面积最大?
,使得绿化面积最大?
查看答案和解析>>
科目:高中数学 来源:2011年江苏省连云港市赣榆高级中学高一(下)综合练习数学试卷(解析版) 题型:解答题
 米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.
米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.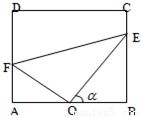
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com