
【题目】设数列{an}的前n项和为Sn , 2Sn=an+1﹣2n+1+1,n∈N* , 且a1 , a2+5,a3成等差数列.
(1)求a1
(2)证明 ![]() 为等比数列,并求数列{an}的通项;
为等比数列,并求数列{an}的通项;
(3)设bn=log3(an+2n),且Tn= ![]() ,证明Tn<1.
,证明Tn<1.
【答案】
(1)解:在 ![]() 中
中
令n=1,得 ![]() ,即a2=2a1+3,①
,即a2=2a1+3,①
令n=2,得 ![]() ,即a3=6a1+13,②
,即a3=6a1+13,②
又2(a2+5)=a1+a3,③
则由①②③解得a1=1
(2)证明:当n≥2时,由 ![]() ,
,
得到 ![]() ,
,
则 ![]() ….
….
由(1)得a2=5,则 ![]() ,
,
∴ ![]() 是以
是以 ![]() 为首项,
为首项, ![]() 为公比的等比数列,
为公比的等比数列,
∴ ![]() ,
,
解得 ![]()
(3)解:∵ ![]() ,则
,则 ![]()
则 ![]()
= ![]()
∴Tn<1
【解析】(1)令n=1,得a2=2a1+3,令n=2,得a3=6a1+13,再由2(a2+5)=a1+a3 , 能求出a1的值.(2)当n≥2时,推导出 ![]() ,从而
,从而 ![]() ,由此能证明
,由此能证明 ![]() 是以
是以 ![]() 为首项,
为首项, ![]() 为公比的等比数列,从而能求出数列{an}的通项.(3)推导出
为公比的等比数列,从而能求出数列{an}的通项.(3)推导出 ![]() ,由此利用裂项求和法能证明Tn<1.
,由此利用裂项求和法能证明Tn<1.
【考点精析】解答此题的关键在于理解等比数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知集合M={x|﹣2<x<2},N={x|x2﹣2x﹣3<0},则集合M∩N=( )
A.{x|x<﹣2}
B.{x|x>3}
C.{x|﹣1<x<2}
D.{x|2<x<3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A1 , A2 , …,A10(如A2表示身高(单位:cm)在[150,155)内的学生人数)图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( ) 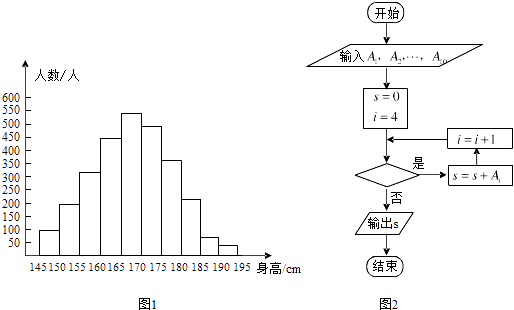
A.i<6
B.i<7
C.i<8
D.i<9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+|x﹣a|+1,x∈R,a∈R.
(Ⅰ)当a=1时,求函数f(x)的最小值;
(Ⅱ)若函数f(x)的最小值为g(a),令m=g(a),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场预算用5600元购买单价为50元(每吨)的钾肥和20元(每吨)的氮肥,希望使两种肥料的总数量(吨)尽可能的多,但氮肥数不少于钾肥数,且不多于钾肥数的1.5倍.
(Ⅰ)设买钾肥x吨,买氮肥y吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(Ⅱ)已知A(10,0),O是坐标原点,P(x,y)在(Ⅰ)中的可行域内,求  的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com