
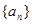 ,
,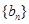 ,且满足
,且满足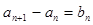 (
(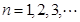 ).
).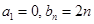 ,求数列
,求数列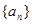 的通项公式;
的通项公式;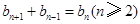 ,且
,且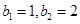 .记
.记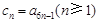 ,求证:数列
,求证:数列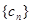 为常数列;
为常数列;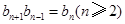 ,且
,且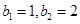 .若数列
.若数列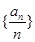 中必有某数重复出现无数次,求首项
中必有某数重复出现无数次,求首项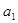 应满足的条件.
应满足的条件.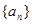 的通项为
的通项为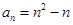 . (2)见解析;
. (2)见解析;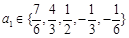 时,数列
时,数列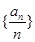 中必有某数重复出现无数次.
中必有某数重复出现无数次. 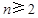 时,有累加法得到
时,有累加法得到
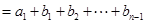
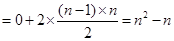 ,
,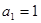 也满足上式,
也满足上式,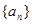 的通项为
的通项为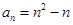 .
. 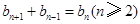 ,
,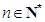 有
有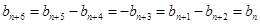 ,
, 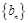 是一个以6为周期的循环数列
是一个以6为周期的循环数列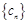 为常数列
为常数列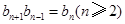 ,且
,且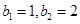 ,所以
,所以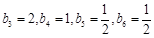 ,
,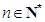 ,有
,有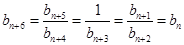 ,
, 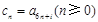 ,(其中
,(其中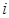 为常数且
为常数且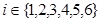 ),所以
),所以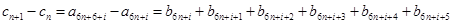
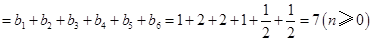 ,
,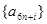 均为以7为公差的等差数列.记
均为以7为公差的等差数列.记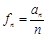 ,构造新数列来分析周期性和最值问题。
,构造新数列来分析周期性和最值问题。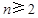 时,有
时,有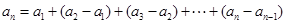
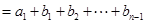 ……………………1分
……………………1分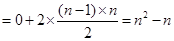 ,
,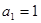 也满足上式,
也满足上式,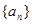 的通项为
的通项为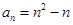 . ………………………………………………………3分
. ………………………………………………………3分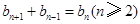 ,
,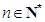 有
有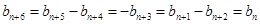 ,
, 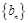 是一个以6为周期的循环数列……………………………………………………5分
是一个以6为周期的循环数列……………………………………………………5分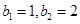 ,所以
,所以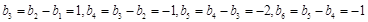
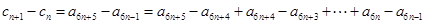

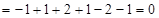
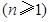 ,
,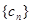 为常数列. ……………………………………………………………………7分
为常数列. ……………………………………………………………………7分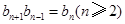 ,且
,且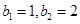 ,所以
,所以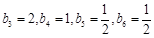 ,
,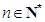 ,有
,有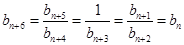 ,
, 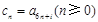 ,(其中
,(其中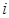 为常数且
为常数且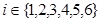 ),所以
),所以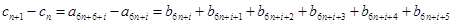
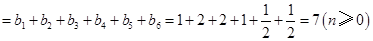 ,
,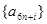 均为以7为公差的等差数列.……………………………………………10分
均为以7为公差的等差数列.……………………………………………10分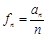 ,则
,则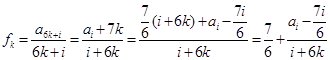 ,
,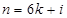
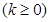 ,
,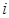 为
为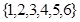 中的一个常数),
中的一个常数),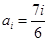 时,对任意的
时,对任意的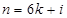 有
有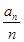
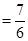 ;…………………………………………12分
;…………………………………………12分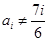 时,
时,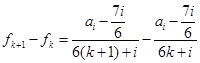
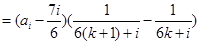
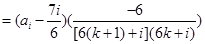
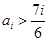 ,则对任意的
,则对任意的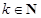 有
有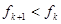 ,数列
,数列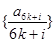 为单调减数列;
为单调减数列;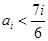 ,则对任意的
,则对任意的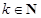 有
有 ,数列
,数列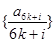 为单调增数列;
为单调增数列;  时,数列
时,数列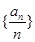 中必有某数重复出现无数次……………14分
中必有某数重复出现无数次……………14分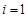 时,
时,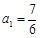 符合要求;当
符合要求;当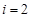 时,
时,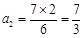 符合要求,此时的
符合要求,此时的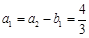 ;
;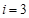 时,
时, 符合要求,此时的
符合要求,此时的 ;
;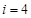 时,
时,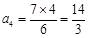 符合要求,此时的
符合要求,此时的 ;
;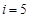 时,
时,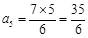 符合要求,此时的
符合要求,此时的 ;
;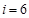 时,
时,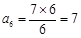 符合要求,此时的
符合要求,此时的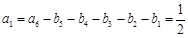 ;
;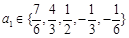 时,数列
时,数列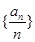 中必有某数重复出现无数次.………………………16分
中必有某数重复出现无数次.………………………16分

科目:高中数学 来源:不详 题型:单选题

 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )| A.6026 | B.6024 | C.2 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 是等和数列,
是等和数列, =3,公和是5,则此数列的前805项的和为 .
=3,公和是5,则此数列的前805项的和为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com