
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
分析 由等比数列的前n项和公式列出方程组求出首项和公比,由此利用经数列前n项和公式能求出$\frac{{{a_2}+{a_{2016}}}}{{{a_1}+{a_{2015}}}}$的值.
解答 解:∵等比数列{an}的前n项和为Sn,S3=1,S6=9,
∴$\left\{\begin{array}{l}{\frac{{a}_{1}(1-{q}^{3})}{1-q}=1}\\{\frac{{a}_{1}(1-{q}^{6})}{1-q}=9}\end{array}\right.$,解得a1=$\frac{1}{7}$,q=2,
∴$\frac{{{a_2}+{a_{2016}}}}{{{a_1}+{a_{2015}}}}$=$\frac{\frac{2}{7}+\frac{{2}^{2015}}{7}}{\frac{1}{7}+\frac{{2}^{2014}}{7}}$=$\frac{2(1+{2}^{2014})}{1+{2}^{2014}}$=2.
故选:C.
点评 本题考查等比数列的性质的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
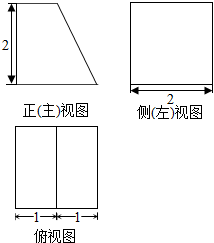
| A. | $16+2\sqrt{3}$ | B. | $16+2\sqrt{5}$ | C. | $20+2\sqrt{3}$ | D. | $20+2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
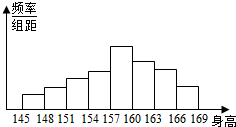 为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三个小组的频数为6.
为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三个小组的频数为6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈N+,2x<2 | B. | ?x∉N+,2x<2 | C. | ?x∉N+,2x<2 | D. | ?x∈N+,2x<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com