
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1) 见解析(2)![]()
【解析】分析:(1)结合题中所给的条件,利用面面垂直的条件以及题中所给的特殊几何图形,得到相应的垂直关系,之后借助于线面垂直来得到线线垂直.
(2)对于存在性问题,可先假设存在,即假设线段![]() 上存在点
上存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,再通过建立空间直角坐标系,求出相关点的坐标,结合向量的数量积求出二面角
,再通过建立空间直角坐标系,求出相关点的坐标,结合向量的数量积求出二面角![]() 的大小,若出现矛盾,则说明假设不成立,即不存在,否则存在.
的大小,若出现矛盾,则说明假设不成立,即不存在,否则存在.
详解:(1)证明:连接![]() ,
,
∵![]() ,
,![]() ,∴△
,∴△![]() 为等边三角形,
为等边三角形,
又∵![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∵![]() 为矩形,∴
为矩形,∴![]() ,
,
又∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(2)由(1)知![]() 平面
平面![]() ,
,
∵![]() 、
、![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,
,
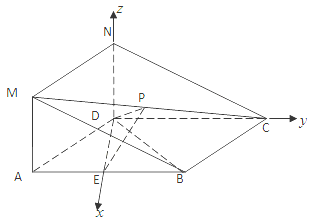
又∵![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]() ,
,
则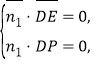 即
即![]() 令
令![]() ,则
,则![]() ,
,
由图形知,平面![]() 的一个法向量
的一个法向量![]() ,
,
由题意知![]() ,
,
即![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】在公园游园活动中有这样一个游戏项目:甲箱子里装有3个白球和2个黑球,乙箱子里装有1个白球和2个黑球,这些球除颜色外完全相同;每次游戏都从这两个箱子里各随机地摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)在一次游戏中:①求摸出3个白球的概率;②求获奖的概率;
(2)在两次游戏中,记获奖次数为X:①求X的分布列;②求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若四面体![]() 的三组对棱分别相等,即
的三组对棱分别相等,即![]() ,
,![]() ,
,![]() ,则________.(写出所有正确结论的编号)
,则________.(写出所有正确结论的编号)
①四面体![]() 每个面的面积相等
每个面的面积相等
②四面体![]() 每组对棱相互垂直
每组对棱相互垂直
③连接四面体![]() 每组对棱中点的线段相互垂直平分
每组对棱中点的线段相互垂直平分
④从四面体![]() 每个顶点出发的三条棱的长都可以作为一个三角形的三边长
每个顶点出发的三条棱的长都可以作为一个三角形的三边长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人用一网箱饲养中华鲟,研究表明:一个饲养周期,该网箱中华鲟的产量![]() (单位:百千克)与购买饲料费用
(单位:百千克)与购买饲料费用![]() (
(![]() )(单位:百元)满足:
)(单位:百元)满足:![]() .另外,饲养过程中还需投入其它费用
.另外,饲养过程中还需投入其它费用![]() .若中华鲟的市场价格为
.若中华鲟的市场价格为![]() 元/千克,全部售完后,获得利润
元/千克,全部售完后,获得利润![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,利润最大,最大利润是多少元?
为何值时,利润最大,最大利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,i是虚数单位,命题p:在复平面内,复数z1=a+ ![]() 对应的点位于第二象限;命题q:复数z2=a﹣i的模等于2,若p∧q是真命题,则实数a的值等于( )
对应的点位于第二象限;命题q:复数z2=a﹣i的模等于2,若p∧q是真命题,则实数a的值等于( )
A.﹣1或1
B.![]() 或
或 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知a1>1,an+1=an2﹣an+1(n∈N*),且 ![]()
![]() +…+
+…+ ![]() =2.则当a2016﹣4a1取得最小值时,a1的值为= .
=2.则当a2016﹣4a1取得最小值时,a1的值为= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元. (Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,n∈N)的函数解析式f(n);
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮胎集团有限公司生产的轮胎的宽度![]() (单位:
(单位: ![]() )服从正态分布
)服从正态分布![]() ,公司规定:轮胎宽度不在
,公司规定:轮胎宽度不在![]() 内将被退回生产部重新生产.
内将被退回生产部重新生产.
(1)求此轮胎不被退回的概率(结果精确到![]() );
);
(2)现在该公司有一批轮胎需要进行初步质检,检验方案是从这批轮胎中任取![]() 件作检验,这
件作检验,这![]() 件产品中至少有
件产品中至少有![]() 件不被退回生产部,则称这批轮胎初步质检合格.
件不被退回生产部,则称这批轮胎初步质检合格.
()求这批轮胎初步质检合格的概率;
()若质检部连续质检了![]() 批轮胎,记
批轮胎,记![]() 为这
为这![]() 批轮胎中初步质检合格的批数,求
批轮胎中初步质检合格的批数,求![]() 的数学期望.
的数学期望.
附:若![]() ,则
,则![]()
![]()
![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com