[题目]若实数a.b.c.d满足︱b+a2-3lna︱+(c-d+2)2=0,则(a-c)2+(b-d)2的最小值为 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】若实数a，b，c，d满足︱b+a2-3lna︱+（c-d+2）2=0,则（a-c）2+（b-d）2的最小值为 .

【答案】8

【解析】

∵实数a、b、c、d满足：（b+a2-3lna）2+（c-d+2）2=0，∴b+a2-3lna=0，c-d+2=0，设b=y，a=x，则y=3lnx-x2，设c=x，d=y，则y=x+2，

∴（a-c）2+（b-d）2就是曲线y=3lnx-x2与直线y=x+2之间的最小距离的平方值.对曲线y=3lnx-x2求导：y'（x）=，与y=x+2平行的切线斜率k=1=，解得x=1或x=-（舍）

把x=1代入y=3lnx-x2，得y=－1，即切点为（1，-1）切点到直线y=x+2的距离：

∴（a-c）2+（b-d）2的最小值就是8．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥中，底面为直角梯形，，，平面底面，为的中点，是棱上的点，，，．

（1）求证：平面平面；

（2）若，求二面角的大小．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数．

（1）当a＝3时，求函数y＝f（x）的图象在x＝0处的切线方程；

（2）当x≥0时，f（x）≥0恒成立，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了解高三学生的“理科综合”成绩是否与性别有关，某校课外学习兴趣小组在本地区高三年级理科班中随机抽取男、女学生各100名，然后对这200名学生在一次联合模拟考试中的“理科综合”成绩进行统计规定：分数不小于240分为“优秀”小于240分为“非优秀”．

（1）根据题意，填写下面的2×2列联表，并根据列联表判断是否有90%以上的把握认为“理科综合”成绩是否优秀与性别有关．

性别	优秀	非优秀	总计
男生	35
女生		75
总计

（2）用分层抽样的方法从成绩优秀的学生中随机抽取12名学生，然后再从这12名学生中抽取3名参加某高校举办的自主招生考试，设抽到的3名学生中女生的人数为X，求X的分布列及数学期望．

附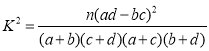：，其中．

	0.10	0.05	0.025	0.010	0.005	0.001
	2.706	3.841	5.024	6.635	7.879	10.828

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积的经验公式为：.弧田（如图1阴影部分）由圆弧和其所对弦围成，弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差.类比弧田面积公式得到球缺(如图 2)近似体积公式：圆面积矢.球缺是指一个球被平面截下的一部分，厦门嘉庚体育馆近似球缺结构（如图3)，若该体育馆占地面积约为18000，建筑容积约为340000，估计体育馆建筑高度(单位：)所在区间为（）

参考数据: ，，，

，.

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数.

(1) 讨论的单调性；

(2) 设，当时，，求的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

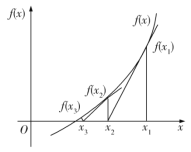
【题目】牛顿迭代法（Newton's method）又称牛顿–拉夫逊方法（Newton–Raphsonmethod），是牛顿在17世纪提出的一种近似求方程根的方法.如图，设是的根，选取作为初始近似值，过点作曲线的切线与轴的交点的横坐标，称是的一次近似值，过点作曲线的切线，则该切线与轴的交点的横坐标为，称是的二次近似值.重复以上过程，直到的近似值足够小，即把作为的近似解.设构成数列.对于下列结论：