Question

对于四面体ABCD ，给出下列四个命题：①若AB=AC，BD=CD，则BC⊥AD;②若AB=CD，AC=BD，则BC⊥AD;③若AB⊥AC，BD⊥CD，则BC⊥AD;④若AB⊥CD，BD⊥AC，则BC⊥AD.其中真命题的序号是__________（写出所有真命题的序号）.

Answer 1

①④?

解析：①为真命题，证明如下：如图，取BC中点M，连结AM、DM.?

由AB=AC，DB=DC，得AM⊥BC，DM⊥BC.?

故BC⊥面AMD，BC⊥AD.所以命题①为真命题.?

④为真命题，证明如下：设点A在平?

面BCD上的射影为点H，连结AH、BH、CH、DH,如图所示.?

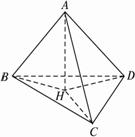
由AH⊥面BCD，AB⊥CD，得BH⊥CD.同理可得CH⊥BD.?

故H为△BCD的垂心，得HD⊥BC.?

又由三垂线定理逆定理可知BC⊥AD.所以命题④为真命题.?

②③都是假命题，可用特例结合反证法来证明.?

如图，设AB=CD=1，AC=BD=2，AB⊥AC，BD⊥CD，作AN⊥BC于N，连结ND.假设BC⊥AD,则BC⊥平面NAD,得BC⊥ND.?

在Rt△ABC中，BN=，??

在Rt△BDC中，BN=，两者相矛盾，假设不正确，即命题②③都是假命题.?

综上，真命题的序号是①④.