
【题目】手机运动计步已成为一种时尚,某中学统计了该校教职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
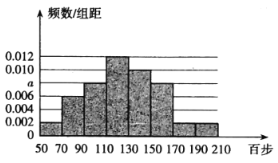
(Ⅰ)求直方图中![]() 的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
(Ⅱ)若该校有教职工175人,试估计一天行走步数不大于130百步的人数;
(Ⅲ)在(Ⅱ)的条件下该校从行走步数大于150百步的3组教职工中用分层抽样的方法选取6人参加远足活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
【答案】(Ⅰ)![]() ,中位数为125;(Ⅱ)98;(Ⅲ)
,中位数为125;(Ⅱ)98;(Ⅲ)![]()
【解析】
(Ⅰ)利用各小矩形的面积之和为1即可得到a,中位数的估计值是小矩形面积和为![]() 时的x的值;
时的x的值;
(Ⅱ)先算出一天步行数不大于130百步的的概率(前4个小矩形的面积之和),再乘以人数175即可;
(Ⅲ)先由分层抽样确定出每组抽取的人数,再结合古典概型的概率计算公式计算即可.
(Ⅰ)由题意得
![]() ,
,
解得![]() ,设中位数为
,设中位数为![]() ,则
,则
![]() 解得
解得![]() ,所以中位数为125.
,所以中位数为125.
(Ⅱ)由![]() ,
,
所以估计一天步行数不大于130百步的人数为98人.
(Ⅲ)在区间![]() 中有28人,在区间
中有28人,在区间![]() 中有7人,在区间
中有7人,在区间![]() 中有7
中有7
人,按分层抽样抽取6人,则从![]() 抽取4人,
抽取4人,![]() 和
和![]() 中各抽取1
中各抽取1
人,设从![]() 抽取
抽取![]() ,从
,从![]() 中抽B,从
中抽B,从![]() 中抽C,则从6
中抽C,则从6
人中抽取2人的情况有:
![]() 共15种情况,
共15种情况,
其中满足两人均来自区间![]() 的有
的有![]() ,共6种情况,
,共6种情况,
所以概率![]() ,所以两人均来自区间
,所以两人均来自区间![]() 的概率为
的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和
和![]() 轴上的定点
轴上的定点![]() ,过抛物线焦点作一条直线交
,过抛物线焦点作一条直线交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() 并延长,交
并延长,交![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求证:直线![]() 过定点;
过定点;
(2)求直线![]() 与直线
与直线![]() 最大夹角为
最大夹角为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为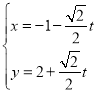 (其中
(其中![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,且
为常数,且![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调节高三学生学习压力,某校高三年级举行了拔河比赛,在赛前三位老师对前三名进行了预测,于是有了以下对话:老师甲:“7班男生比较壮,7班肯定得第一名”.老师乙:“我觉得14班比15班强,14班名次会比15班靠前”.老师丙:“我觉得7班能赢15班”.最后老师丁去观看完了比赛,回来后说:“确实是这三个班得了前三名,且无并列,但是你们三人中只有一人预测准确”.那么,获得一、二、三名的班级依次为( )
A.7班、14班、15班B.14班、7班、15班
C.14班、15班、7班D.15班、14班、7班
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 垂直于
垂直于![]() 所在的平面
所在的平面![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() 是弧
是弧![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合),
重合),![]() 为
为![]() 上一点,且
上一点,且![]() 是线段
是线段![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合).
重合).
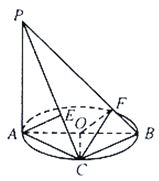
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是弧
是弧![]() 的中点,
的中点,![]() 是锐角,且三棱锥
是锐角,且三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱ABC﹣A1B1C1中,平面AA1B1B⊥平面ABC,AB=AA1=A1B=4,BC=2,AC=2![]() ,点F为AB的中点,点E为线段A1C1上的动点.
,点F为AB的中点,点E为线段A1C1上的动点.
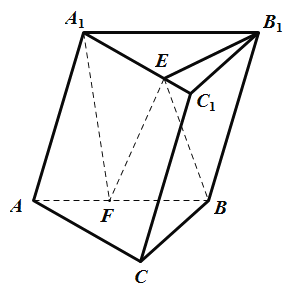
(1)求证:BC⊥平面A1EF;
(2)若∠B1EC1=60°,求四面体A1B1EF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点左边)与直线
点左边)与直线![]() 交于点
交于点![]() .求
.求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() 1(a
1(a![]() 0,b
0,b![]() 0)的左右焦点分别为F1,F2,点O为坐标原点,点P在双曲线的右支上,且满足|F1F2|=2|OP|.若直线PF2与双曲线C只有一个交点,则双曲线C的离心率为( )
0)的左右焦点分别为F1,F2,点O为坐标原点,点P在双曲线的右支上,且满足|F1F2|=2|OP|.若直线PF2与双曲线C只有一个交点,则双曲线C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com