
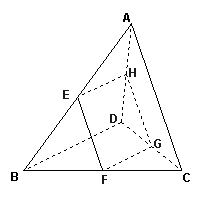
 (历史方向) 如图,空间四边形ABCD中,AC,BD为对角线,E,F分别为AB,BC的中点,G,H分别在边CD,DA上,且
(历史方向) 如图,空间四边形ABCD中,AC,BD为对角线,E,F分别为AB,BC的中点,G,H分别在边CD,DA上,且![]() .
.
⑴求证:点E,F,G,H共面;
⑵若λ=2,求证:直线FG,EH,BD相交于一点.
如图,空间四边形ABCD中,AC,BD为对角线,E,F分别为AB,BC的中点,G,H分别在边CD,DA上,且![]() .
.
⑴求证:点E,F,G,H共面;
 ⑵若λ=2,求证:直线FG,EH,BD相交于一点.
⑵若λ=2,求证:直线FG,EH,BD相交于一点.
证明: ⑴∵在△ABC中,E,F分别为AB,BC的中点
∴EF‖AC且![]() ……………………(2分)
……………………(2分)
又∵在△ADC中, G,H分别在边CD,DA上,且![]()
∴GH‖AC且![]() ……………………(4分)
……………………(4分)
∴EF‖GH ……………………(6分)
∴点E,F,G,H共面. ……………………(7分)
⑵当λ=2时,由⑴得![]() ,
,![]() ∴EF>GH ……………………(8分)
∴EF>GH ……………………(8分)
∴FG,EH在平面EFGH内不平行,设FG,EH相交于点O ……………………(9分)
∴O∈FG ……………………(10分)
又∵FG![]() 平面BDC
平面BDC
∴O∈平面BDC ……………………(11分)
同理O∈平面BDA
∴O在平面BDC与平面BDA交线上 ……………………(12分)
又∵平面BDC∩平面BDA=BD
∴O∈BD
∴直线FG,EH,BD相交于一点O. ……………………(14分)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com