已知函数
定义在(―1，1)上，对于任意的
，有
，且当
时，
。
(1)验证函数
是否满足这些条件；
(2)判断这样的函数是否具有奇偶性和单调性，并加以证明；
(3)若
，求方程
的解。
（1）详见解析；（2）奇函数，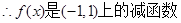
，证明详见解析；（3）x=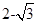
解析试题分析：(1)只要把x、y、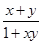
代入函数解析式化简即可得：，然后验证定义域范围符合即可；
（2）可以根据函数的奇偶性和单调性的定义，并利用赋值法，变量代换的方法得到f(－x)=－f(x)为奇函数和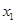
、
时
为减函数；
（3）利用奇函数和，得到
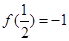和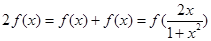
，代入已知方程即可解决.
试题解析：（1）
∴－1<x<1即定义域为(－1,1)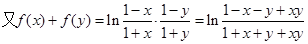
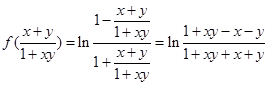
∴成立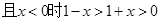
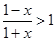
4分
（2）令x=y=0，则f(0)=0，令y=－x则f(x)+f(－x)=0
∴f(－x)=－f(x)为奇函数
任取、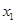
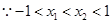
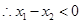
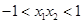
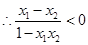
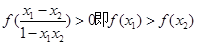
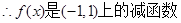8分
（3）∵f(x)为奇函数 ∴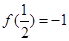
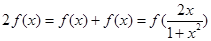
由 
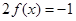
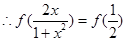
∵f(x)为(－1，1)上单调函数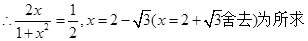 
13分
考点：函数性质的综合应用.
名校课堂系列答案科目：高中数学 来源： 题型：解答题
设命题p：f(x)＝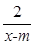
在区间(1，＋∞)上是减函数；命题q：x1，x2是方程x2－ax－2＝0的两个实根，且不等式m2＋5m－3≥|x1－x2|对任意的实数a∈[－1,1]恒成立．若
p∧q为真，试求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，两个工厂A、B相距2km，点O为AB的中点，要在以O为圆心，2km为半径的圆弧MN上的某一点P处建一幢办公楼，其中MA⊥AB，NB⊥AB.据测算此办公楼受工厂A的“噪音影响度”与距离AP的平方成反比，比例系数为1；办公楼受工厂B的“噪音影响度”与距离BP的平方也成反比，比例系数为4，办公楼与A、B两厂的“总噪音影响度”y是A、B两厂“噪音影响度”的和，设AP为xkm.
(1)求“总噪音影响度”y关于x的函数关系式，并求出该函数的定义域；
(2)当AP为多少时，“总噪音影响度”最小？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝ex－e－x(x∈R且e为自然对数的底数)．
(1)判断函数f(x)的奇偶性与单调性；
(2)是否存在实数t，使不等式f(x－t)＋f(x2－t2)≥0对一切x都成立？若存在，求出t；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的一元二次函数
，设集合
，分别从集合P和Q中随机取一个数作为
和
有零点的概率；
上是增函数的概率。
.
的解集为
，求
的值；
，使
，求
。
的解集；
对
恒成立，求实数a的取值范围。
对任意实数
恒有
且当
时，有
且
.
上的最大值；
的不等式
.