
分析 (1)求出f(x)的导数,得到x=$\frac{1+\sqrt{5}}{2}$是f′(x)=0的根,代入方程求出a的值即可;
(2)问题转化为lnx-$\frac{1}{2}$(x-1)2-x+1<0在(1,+∞)恒成立,令g(x)=lnx-$\frac{1}{2}$(x-1)2-x+1,x>1,根据函数的单调性求出g(x)>g(1)即可.
解答 解:(1)∵f(x)=1nx-a(x-1)2,
∴f′(x)=$\frac{1}{x}$-2a(x-1),
∴x=$\frac{1+\sqrt{5}}{2}$是f′(x)=0的根,
∴$\frac{2}{1+\sqrt{5}}-2a(\frac{1+\sqrt{5}}{2}-1)=0$,
解得:a=$\frac{1}{2}$;
证明:(2)由(1)得:f(x)=lnx-$\frac{1}{2}$(x-1)2,
当x>1时,f(x)<x-1,
即lnx-$\frac{1}{2}$(x-1)2-x+1<0在(1,+∞)恒成立,
令g(x)=lnx-$\frac{1}{2}$(x-1)2-x+1,x>1,
g′(x)=$\frac{1{-x}^{2}}{x}$<0,(x>1),
∴g(x)在(1,+∞)递减,
∴g(x)>g(1)=0,
故当x>1时,f(x)<x-1成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:选择题
 如图,矩形ABCD与矩形ADEF所在的平面互相垂直,将△DEF沿FD翻折,翻折后的点E(记为点P)恰好落在BC上,设AB=1,FA=x(x>1),AD=y,则以下结论正确的是( )
如图,矩形ABCD与矩形ADEF所在的平面互相垂直,将△DEF沿FD翻折,翻折后的点E(记为点P)恰好落在BC上,设AB=1,FA=x(x>1),AD=y,则以下结论正确的是( )| A. | 当x=2时,y有最小值$\frac{4\sqrt{3}}{3}$ | B. | 当x=2时,有最大值$\frac{4\sqrt{3}}{3}$ | ||
| C. | 当x=$\sqrt{2}$时,y有最小值2 | D. | 当x=$\sqrt{2}$时,y有最大值2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 5 | 6 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 时间代号x | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y (千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
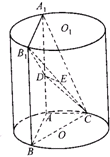 如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,3\sqrt{5})$ | B. | $[-\sqrt{5},\sqrt{5}]$ | C. | $(-3\sqrt{5},3\sqrt{5})$ | D. | $(0,\sqrt{5})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com