
【题目】若函数f(x)=2x2+(x﹣2a)|x﹣a|在区间[﹣3,1]上不是单调函数,则实数a的取值范围是( )
A.[﹣4,1]
B.[﹣3,1]
C.(﹣6,2)
D.(﹣6,1)
【答案】C
【解析】解:当a=1时,f(x)=2x2+(x﹣2)|x﹣1|在[﹣3,1]上,
f(x)=2x2+(x﹣2)(1﹣x)=x2+3x﹣2,
对称轴为x=﹣ ![]() ∈[﹣3,1],可得f(x)在区间[﹣3,1]上不是单调函数;
∈[﹣3,1],可得f(x)在区间[﹣3,1]上不是单调函数;
排除选项D;
当a=﹣5时,f(x)在[﹣3,1]即为f(x)=2x2+(x+10)(x+5)=3x2+15x+50,
对称轴为x=﹣ ![]() ∈[﹣3,1],可得f(x)在区间[﹣3,1]上不是单调函数;
∈[﹣3,1],可得f(x)在区间[﹣3,1]上不是单调函数;
排除选项A,B.
故选:C.
【考点精析】通过灵活运用二次函数的性质,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减即可以解答此题.
上递减即可以解答此题.


科目:高中数学 来源: 题型:
【题目】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是( )
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式V= ![]()
A.2寸
B.3寸
C.4寸
D.5寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax2+x﹣1)ex , 其中e是自然对数的底数,a∈R.
(Ⅰ)若a=1.求曲线f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a=﹣1,函数f(x)的图象与函数g(x)=![]() x3+
x3+![]() x2+m的图象有3个不同的交点,求实数m的取值范围.
x2+m的图象有3个不同的交点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京故宫博物院成立于1925年10月10日,是在明、清朝两代皇宫及其宫廷收藏的基础上建立起来的中国综合性博物馆,每年吸引着大批游客参观游览![]() 下图是从2012年到2017年每年参观人数的折线图
下图是从2012年到2017年每年参观人数的折线图![]() 根据图中信息,下列结论中正确的是
根据图中信息,下列结论中正确的是![]()
![]()
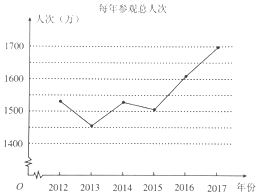
A. 2013年以来,每年参观总人次逐年递增
B. 2014年比2013年增加的参观人次不超过50万
C. 2012年到2017年这六年间,2017年参观总人次最多
D. 2012年到2017年这六年间,平均每年参观总人次超过160万
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C以坐标轴为对称轴,以坐标原点为对称中心,椭圆的一个焦点为![]() ,点
,点![]() 在椭圆上,
在椭圆上,
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程.
求椭圆C的方程.
![]() Ⅱ
Ⅱ![]() 斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|(x﹣2m+1)(x﹣m+2)<0},B={x|1≤x+1≤4}.
(1)若m=1,求A∩B;
(2)若A∩B=A,求实数m的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(1) 求圆![]() 的方程;
的方程;
(2)问是否存在满足以下两个条件的直线![]() :①斜率为
:①斜率为![]() ;②直线被圆
;②直线被圆![]() 截得的弦为
截得的弦为![]() ,以
,以![]() 为直径的圆过原点. 若存在这样的直线,请求出其方程;若不存在,请说明理由.
为直径的圆过原点. 若存在这样的直线,请求出其方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],若成绩大于等于90分的人数为36,则成绩在[110,130)的人数为( ) 
A.12
B.9
C.15
D.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com