
分析 画出图象,根据图象判定(1),(2),对于(3)由图象说明函函数f(x)在($\frac{1}{2}$,+∞)上是单调增函数,f(x)min>0即可,
即f($\frac{1}{2}$)≥0解,得a的取值范围是a≥1;
解答 解:对于(1),由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;
对于(2),由图象说明函函数f(x)在R上不是单调函数;故错;
对于(3)由图象说明函函数f(x)在($\frac{1}{2}$,+∞)上是单调增函数,f(x)min>0即可,
即 f($\frac{1}{2}$)≥0解,得a的取值范围是a≥1;故错;
f($\frac{1}{2}$)≥0解,得a的取值范围是a≥1;故错;
答案为:(1)
点评 利用函数的图象研究函数的单调区间以及根据函数的增减性得到函数的最值是常用的方法,解答本题的关键是图象法


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2x-y+1=0 | B. | x-2y+1=0 | C. | 2x+y+1=0 | D. | 2x-y+2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2)∪(2,+∞) | B. | (2,+∞) | C. | [2,+∞) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
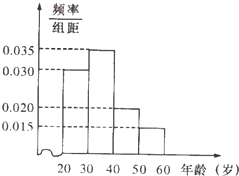 某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.
某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 27 | 16 |
| [30,40) | 28 | 18 |
| [40,50) | 26 | 9 |
| [50,60] | 6 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com