
已知 为
为 的内角
的内角 的对边,满足
的对边,满足 ,函数
,函数
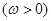 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,证明
,证明 为等边三角形.
为等边三角形.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
如图,在半径为 、圆心角为60°的扇形的
、圆心角为60°的扇形的 弧上任取一点
弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在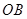 上,设矩形
上,设矩形 的面积为
的面积为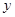 .
.
(Ⅰ) 按下列要求写出函数关系式:
① 设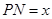 ,将
,将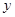 表示成
表示成 的函数关系式;
的函数关系式;
② 设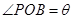 ,将
,将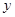 表示成
表示成 的函数关系式.
的函数关系式.
(Ⅱ) 请你选用(Ⅰ)中的一个函数关系式,求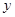 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
阅读下面材料:
根据两角和与差的正弦公式,有 ------①
------① ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明: ;
;
(Ⅱ)若 的三个内角
的三个内角 满足
满足 ,试判断
,试判断 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com