
【题目】如图,在四棱锥![]() 中,
中,![]()
![]() 平面
平面![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
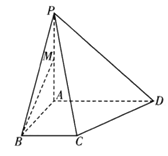
(1)证明:![]() 平面
平面![]()
![]()
(2)当![]() 为何值时,四棱锥
为何值时,四棱锥![]() 的体积最大?并求此最大值
的体积最大?并求此最大值
【答案】(1)见解析(2)当PA=4时,体积最大值为16.
【解析】
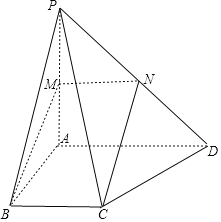
(1)取PD中点N,易证MNCB为平行四边形,进而得BM,CN平行,得证;
(2)设PA=x(0![]() ),把体积表示为关于x的函数,借助不等式求得最大值.
),把体积表示为关于x的函数,借助不等式求得最大值.
(1)取PD中点N,连接MN,CN,
∵M是AP的中点,
∴MN∥AD且MN![]() ,
,
∵AD∥BC,AD=2BC,
∴MN∥BC,MN=BC,
∴四边形MNCB是平行四边形,
∴MB∥CN,
又BM![]() 平面PCD,CN平面PCD,
平面PCD,CN平面PCD,
∴BM∥平面PCD;
(2)设PA=x(0<x<4![]() ),
),
∵PA⊥平面ABCD,
∴PA⊥AB,
∵![]() ,
,
∴AB![]() ,
,
又∵AB⊥AD,AD=2BC=4,
∴VP﹣ABCD![]()
![]()
![]()
![]()
=16,
当且仅当x![]() ,即x=4时取等号,
,即x=4时取等号,
故当PA=4时,四棱锥P﹣ABCD的体积最大,最大值为16.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (其中
(其中![]() 为参数).现以坐标原点为极点,
为参数).现以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 普通方程和曲线
普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() ,且与直线
,且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下所示.
题号 | 分组 | 频数 | 频率 |
第1组 |
| 0.100 | |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
第6组 |
| 100 | 1.00 |
(1)请先求出频率分布表中①、②位置的相应数据,再完成如下的频率分布直方图;

(2)组委会决定在5名(其中第3组2名,第4组2名,第5组1名)选手中随机抽取2名选接受![]() 考官进行面试,求第4组至少有1名选手被考官
考官进行面试,求第4组至少有1名选手被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,平面直角坐标系xOy中,曲线C的参数方程为
,平面直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数).
为参数).
(1)设直线l与曲线C交于M,N两点,求|MN|;
(2)若点P(x,y)为曲线C上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是我国古代的伟大科学家,他在5世纪末提出祖暅:“幂势即同,则积不容异”,意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等. 祖暅原理常用来由已知几何体的体积推导未知几何体的体积,例如由圆锥和圆柱的的体积推导半球体的体积,其示意图如图所示,其中图(1)是一个半径为R的半球体,图(2)是从圆柱中挖去一个圆锥所得到的几何体. (圆柱和圆锥的底面半径和高均为R)

利用类似的方法,可以计算抛物体的体积:在x-O-y坐标系中,设抛物线C的方程为y=1-x2 (-1![]() x
x![]() 1),将曲线C围绕y轴旋转,得到的旋转体称为抛物体. 利用祖暅原理可计算得该抛物体的体积为_________.
1),将曲线C围绕y轴旋转,得到的旋转体称为抛物体. 利用祖暅原理可计算得该抛物体的体积为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的PK赛,![]() 两队各由4名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为
两队各由4名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为![]() ,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计,某蔬菜基地西红柿亩产量的增加量![]() (百千克)与某种液体肥料每亩使用量
(百千克)与某种液体肥料每亩使用量![]() (千克)之间的对应数据的散点图,如图所示.
(千克)之间的对应数据的散点图,如图所示.

(1)依据数据的散点图可以看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(若
并加以说明(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)求![]() 关于
关于![]() 的回归方程,并预测液体肥料每亩使用量为
的回归方程,并预测液体肥料每亩使用量为![]() 千克时,西红柿亩产量的增加量约为多少?
千克时,西红柿亩产量的增加量约为多少?
附:相关系数公式 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com