
【题目】已知等比数列{an}(n=1,2,3)满足an+1=2﹣|an|,若a1>0,则a1=_____.
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
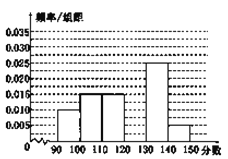
(1)求分数在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() 、
、![]() 和
和![]() ,满足
,满足![]() ,且对任意实数
,且对任意实数![]() 、
、![]() (
(![]() ),恒有
),恒有![]() 成立.
成立.
⑴试写 出一组满足条件的具体的![]() 和
和![]() ,使
,使![]() 为增函数,
为增函数,![]() 为减函数,但
为减函数,但![]() 为增函数.
为增函数.
⑵判断下列两个命题的真假,并说明理由.
命题1):若![]() 为增函数,则
为增函数,则![]() 为增函数;
为增函数;
命题2):若![]() 为增函数,则
为增函数,则![]() 为增函数.
为增函数.
⑶已知![]() ,写出一组满足条件的具体的
,写出一组满足条件的具体的![]() 和
和![]() ,且
,且![]() 为非常值函数,并说明理由.
为非常值函数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为非空实数集(至少有两个元素),若对任意
为非空实数集(至少有两个元素),若对任意![]() ,都有
,都有![]() ,且
,且![]() ,则称
,则称![]() 为封闭集,则下列四个判断:
为封闭集,则下列四个判断:
①集合![]() 为封闭集,则
为封闭集,则![]() 为无限集; ②集合
为无限集; ②集合![]() 为封闭集;
为封闭集;
③若集合![]() 为封闭集,则
为封闭集,则![]() 为封闭集; ④若
为封闭集; ④若![]() 为封闭集,则一定有
为封闭集,则一定有![]() ;,
;,
其中正确的命题个数有( ).
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市实施全域旅游,将乡村旅游公路建设与特色田园乡村发展结合,精心打造全长365公里的“1号公路”,对内串联区域内主要景区景点和自然村,对外通达周边县(市),以路引景、为景串线,形成一个“大环小圈、内连外引”的路网体系.如今的“1号公路”,不仅成为该市旅游业的“颜值担当”,更成为推动乡村振兴的“实力担当”,农村居住环境日益改善,新农村别墅随处可见.图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面
市实施全域旅游,将乡村旅游公路建设与特色田园乡村发展结合,精心打造全长365公里的“1号公路”,对内串联区域内主要景区景点和自然村,对外通达周边县(市),以路引景、为景串线,形成一个“大环小圈、内连外引”的路网体系.如今的“1号公路”,不仅成为该市旅游业的“颜值担当”,更成为推动乡村振兴的“实力担当”,农村居住环境日益改善,新农村别墅随处可见.图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面![]() 和
和![]() 是全等的等腰梯形,左右两坡屋面
是全等的等腰梯形,左右两坡屋面![]() 和
和![]() 是全等的三角形.点
是全等的三角形.点![]() 在平面
在平面![]() 和
和![]() 上的射影分别为
上的射影分别为![]() (即:
(即:![]() 平面
平面![]() ,垂足为
,垂足为![]() ;
;![]() ,垂足为
,垂足为![]() ).已知
).已知![]() ,梯形
,梯形![]() 的面积是
的面积是![]() 面积的2.2倍.
面积的2.2倍.![]() .
.

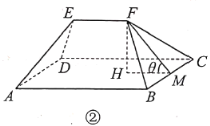
(1)当![]() 时,求屋顶面积的大小;
时,求屋顶面积的大小;
(2)求屋顶面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)已知上部屋顶造价与屋顶面积成正比,比例系数为![]() (
(![]() 为正的常数),下部主体造价与其高度成正比,比例系数为
为正的常数),下部主体造价与其高度成正比,比例系数为![]() .现欲造一栋上、下总高度为
.现欲造一栋上、下总高度为![]() 的别墅,试问:当
的别墅,试问:当![]() 为何值时,总造价最低?
为何值时,总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,
中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,M是线段AB的中点.
,M是线段AB的中点.
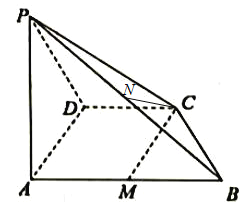
(1)求证:![]() 平面PAB;
平面PAB;
(2)已知点N是线段PB的中点,试判断直线CN与平面PAD的位置关系,并证明你的判断.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数,下列关于
的最大整数,下列关于![]() 说法正确的有:______.
说法正确的有:______.
①![]() 的值域为[-1,1]
的值域为[-1,1]
②![]() 为奇函数
为奇函数
③![]() 为周期函数,且最小正周期T=4
为周期函数,且最小正周期T=4
④![]() 在[0,2)上为单调增函数
在[0,2)上为单调增函数
⑤![]() 与
与![]() 的图像有且仅有两个公共点
的图像有且仅有两个公共点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com