
【题目】随着银行业的不断发展,市场竞争越来越激烈,顾客对银行服务质量的要求越来越高,银行为了提高柜员员工的服务意识,加强评价管理,工作中让顾客对服务作出评价,评价分为满意、基本满意、不满意三种.某银行为了比较顾客对男女柜员员工满意度评价的差异,在下属的四个分行中随机抽出40人(男女各半)进行分析比较.对40人一月中的顾客评价“不满意”的次数进行了统计,按男、女分为两组,再将每组柜员员工的月“不满意”次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下频数分布表.
,得到如下频数分布表.
分组 |
|
|
|
|
|
女柜员 | 2 | 3 | 8 | 5 | 2 |
男柜员 | 1 | 3 | 9 | 4 | 3 |
(1)在答题卡所给的坐标系中分别画出男、女柜员员工的频率分布直方图;分别求出男、女柜员员工的月平均“不满意”次数的估计值,试根据估计值比较男、女柜员员工的满意度谁高?
(2)在抽取的40名柜员员工中:从“不满意”次数不少于20的员工中随机抽取3人,并用X表示随机抽取的3人中女柜员工的人数,求X的分布列和数学期望.
【答案】(1)直方图见解析;男、女柜员月平均“不满意”次数的估计值分别为![]() ,
,![]() ;女柜员员工的满意度高;(2)分布列见解析,
;女柜员员工的满意度高;(2)分布列见解析,![]()
【解析】
(1)分别列出女柜员、男柜员的频率分布表,再画出女柜员、男柜员的频率分布直方图;计算女柜员、男柜员员工的月平均“不满意”次数,比较即可得出结论.
(2)在抽取的40名柜员员工中,“不满意”次数不少于20的柜员员工共有5人,其中女员工2人,男员工3人,从“不满意”次数不少于20的柜员员工中随机抽取3人,故X的所有可能取值为0,1,2,分别写出分布列,求出数学期望值.
(1)对于女柜员列出频率分布表如下,
分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25] |
女柜员 | 2 | 3 | 8 | 5 | 2 |
频率 | 0.1 | 0.15 | 0.4 | 0.25 | .0.1 |
对于男柜员列出频率分布表如下;
分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25] |
男柜员 | 1 | 3 | 9 | 4 | 3 |
男柜员 | 0.05 | 0.15 | 0.45 | 0.2 | 0.15 |
分别求出每组的频率,画出的直方图如图.
女柜员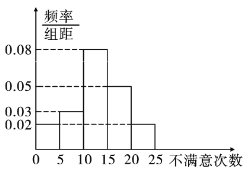 男柜员
男柜员 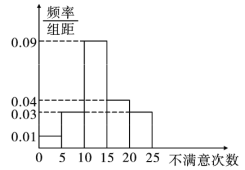
设女、男柜员员工的月平均“不满意”次数分别为![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,所以女柜员员工的满意度比男柜员员工的满意度要高.
,所以女柜员员工的满意度比男柜员员工的满意度要高.
(2)在抽取的40名柜员员工中,“不满意”次数不少于20的柜员员工共有5人,其中女员工2人,男员工3人,
从“不满意”次数不少于20的柜员员工中随机抽取3人,故X的所有可能取值为0,1,2,
则![]() ,
,![]() ,
,![]() ,
,
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】中学为研究学生的身体素质与体育锻炼时间的关系,对该校200名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
并通过计算判断,是否能在犯错误的概率不超过0.025的前提下认为“锻炼达标”与性别有关?
(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出10人,进行体育锻炼体会交流,
(i)求这10人中,男生、女生各有多少人?
(ii)从参加体会交流的10人中,随机选出2人作重点发言,记这2人中女生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试,若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.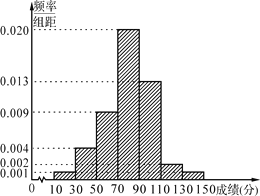
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南某地区![]() 年10年间梅雨季节的降雨量
年10年间梅雨季节的降雨量![]() 单位:
单位:![]() 的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
的频率分布直方图,试用样本频率估计总体概率,解答下列问题:

![]() 假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
![]() 老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元
老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元![]() 而乙品种杨梅的亩产量
而乙品种杨梅的亩产量![]() 亩
亩![]() 与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为
与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为![]() 元
元![]() ,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润
,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润![]() 万元
万元![]() 的期望更大?并说明理由.
的期望更大?并说明理由.
降雨量 |
|
|
|
|
亩产量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
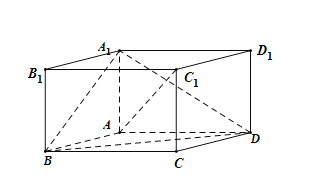
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为了帮助当地农民脱贫致富,开发了一种新型水果类食品,该食品生产成本为每件8元.当天生产当天销售时,销售价为每件12元,当天未卖出的则只能卖给水果罐头厂,每件只能卖5元.每天的销售量与当天的气温有关,根据市场调查,若气温不低于![]() ,则销售5000件;若气温位于
,则销售5000件;若气温位于![]() ,则销售3500件;若气温低于
,则销售3500件;若气温低于![]() ,则销售2000件.为制定今年8月份的生产计划,统计了前三年8月份的气温范围数据,得到下面的频数分布表:
,则销售2000件.为制定今年8月份的生产计划,统计了前三年8月份的气温范围数据,得到下面的频数分布表:
气温范围 (单位: |
|
|
|
|
|
天数 | 4 | 14 | 36 | 21 | 15 |
以气温范围位于各区间的频率代替气温范围位于该区间的概率.
(1)求今年8月份这种食品一天销售量(单位:件)的分布列和数学期望值;
(2)设8月份一天销售这种食品的利润为![]() (单位:元),当8月份这种食品一天生产量
(单位:元),当8月份这种食品一天生产量![]() (单位:件)为多少时,
(单位:件)为多少时,![]() 的数学期望值最大,最大值为多少
的数学期望值最大,最大值为多少![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com