
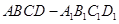 中,侧面
中,侧面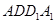 ⊥底面
⊥底面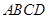 ,
, ,底面
,底面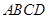 为直角梯形,其中
为直角梯形,其中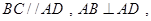
 ,O为
,O为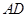 中点.
中点.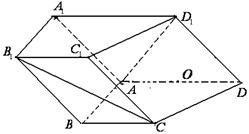
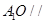 平面
平面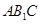 ;
; 。
。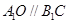 ,即证:四边形AB1CO为平行四边形.
,即证:四边形AB1CO为平行四边形.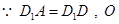 为
为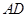 的中点,
的中点,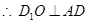 ,又侧面
,又侧面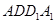 ⊥底面
⊥底面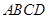 ,故
,故 ⊥底面
⊥底面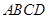 ,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.
,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.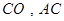 , …………..1分
, …………..1分 为正方形, …………..2分
为正方形, …………..2分 ,且
,且
 为平行四边形,…………..3分
为平行四边形,…………..3分 , …………..4分
, …………..4分 平面
平面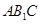 ,
,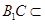 平面
平面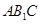 ……..5分
……..5分 平面
平面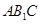 …………..6分
…………..6分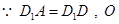 为
为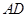 的中点,
的中点,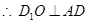 ,又侧面
,又侧面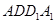 ⊥底面
⊥底面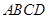 ,故
,故 ⊥底面
⊥底面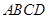 ,…………..7分
,…………..7分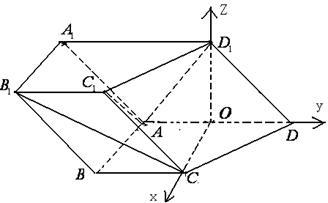
 为原点,所
为原点,所 在直线分别为
在直线分别为 轴,
轴, 轴,
轴,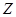 轴建立如图所示的坐标系,则
轴建立如图所示的坐标系,则
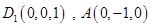 ,…………..8分
,…………..8分
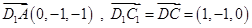 ,…………..9分
,…………..9分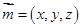 为平面
为平面 的一个法向量,由
的一个法向量,由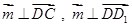 ,得
,得 ,
,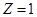 ,则
,则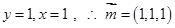 ………..10分
………..10分 为平面
为平面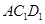 的一个法向量,由
的一个法向量,由 ,得
,得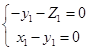 ,令
,令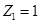 ,则
,则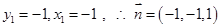 ,………..11分
,………..11分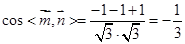 ,故所求锐二面角A—C1D1—C的余弦值为
,故所求锐二面角A—C1D1—C的余弦值为 ………..12分
………..12分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
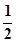 AD=1,CD=
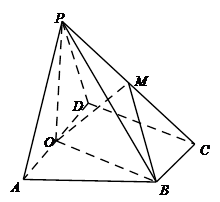
AD=1,CD=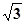 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
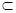 M,b
M,b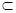 M,且c⊥a,c⊥b,则c⊥M ④若a⊥M, a//N,则M⊥N,其中正确命题的个数为( )
M,且c⊥a,c⊥b,则c⊥M ④若a⊥M, a//N,则M⊥N,其中正确命题的个数为( )| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.平面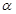 内的一条直线 内的一条直线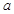 垂直与平面 垂直与平面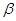 内的无数条直线,则 内的无数条直线,则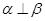 |
B.若直线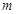 与平面 与平面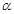 内的一条直线平行,则 内的一条直线平行,则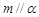 |
C.若平面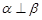 ,且 ,且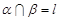 ,则过 ,则过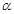 内一点 内一点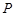 与 与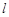 垂直的直线垂直于平面 垂直的直线垂直于平面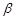 |
D.若直线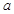 与平面 与平面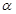 内的无数条直线都垂直,则不能说一定有 内的无数条直线都垂直,则不能说一定有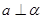 . . |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 与平面
与平面 平行的是( )
平行的是( )A. 、 、 都垂直于平面 都垂直于平面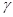 |
B. 内存在不共线的三点到平面 内存在不共线的三点到平面 的距离相等 的距离相等 |
C.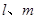 是 是 内两条直线,且 内两条直线,且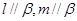 |
D.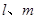 是两条异面直线,且 是两条异面直线,且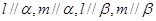 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com