【题目】已知
的内角
所对的边分别为
，_________，且
.现从：①
，②
，③
这三个条件中任选一个，补充在以上问题中，并判断这样的是否存在，若存在，求的面积
_________；若不存在，请说明理由.
一课一练课时达标系列答案科目：高中数学 来源： 题型：
【题目】如图，平面
平面
，
，四边形为平行四边形，
，
为线段
的中点，点
满足
.
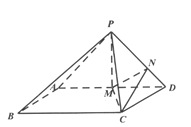
（Ⅰ）求证：直线
平面
；
（Ⅱ）求证：平面
平面
；
（Ⅲ）若平面
平面
，求直线
与平面所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=aex，g（x）=lnx-lna，其中a为常数，且曲线y=f（x）在其与y轴的交点处的切线记为l1，曲线y=g（x）在其与x轴的交点处的切线记为l2，且l1∥l2．
（1）求l1，l2之间的距离；
（2）若存在x使不等式
成立，求实数m的取值范围；
（3）对于函数f（x）和g（x）的公共定义域中的任意实数x0，称|f（x0）-g（x0）|的值为两函数在x0处的偏差．求证：函数f（x）和g（x）在其公共定义域内的所有偏差都大于2．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直三棱柱
中，
，底面三边长分别为3，5，7，
是上底面
所在平面内的动点，若三棱锥
的外接球表面积为
，则满足题意的动点的轨迹对应图形的面积为________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的参数方程为
（
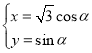为参数），以原点
为极点，以
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
.
（1）求曲线的普通方程与曲线的直角坐标方程；
（2）设
为曲线上位于第一，二象限的两个动点，且
，射线
交曲线分别于
，求
面积的最小值，并求此时四边形
的面积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】20名学生某次数学考试成绩(单位：分)的频率分布直方图如下：
(1)求频率直方图中a的值；
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数；
(3)从成绩在[50,70)的学生中人选2人，求这2人的成绩都在[60,70)中的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】己知p：函数f（x）在R上是增函数，f（m2）＜f（m+2）成立；q：方程
1（m∈R）表示双曲线．
（1）若p为真命题，求m的取值范围；
（2）若p∨q为真，p∧q为假，求m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】平面直角坐标系
中，曲线
的参数方程为
（
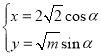为参数），以原点为极点，
轴为非负半轴建立极坐标系，直线
的极坐标方程为
.
（1）求直线的直角坐标方程和曲线的普通方程；
（2）求直线与曲线交于两点
，线段
的中点的横坐标为
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】等差数列
中，
，
，
分别是下表第一、二、三行中的某一个数，且其中的任何两个数不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | 5 | 8 | 2 |
第二行 | 4 | 3 | 12 |
第三行 | 16 | 6 | 9 |
（1）请选择一个可能的
组合，并求数列
的通项公式；
（2）记（1）中您选择的的前
项和为
，判断是否存在正整数
，使得，
，
成等比数列，若有，请求出的值；若没有，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
