
解析几何并不是一门独立的学科,很多问题的解决都离不开我们初中学过的平面几何的性质.请想想下面的问题该怎么求解?其中要运用哪些平面几何的知识?
值.
已知圆(x-2)2+y2=1,求点(-2,-3)与圆上的点的距离的最大值与最小
|
如图所示,点A(-2,-3),圆的圆心O(2,0),连结AO,则这条直线与圆交于两点B、C,由平面几何知识,点A与圆上点的距离的最小值应该是线段AB的长,点A与圆上点的最大值应该是线段AC的长.它们的长度分别是线段AO的长减去和加上圆的半径的长.应用两点间的距离公式得AO=5,又圆的半径为1,所以AB=4,AC=6.
所以点(-2,-3)与圆上的点的距离的最大值与最小值分别是6和4. |
|
处理圆的有关问题,往往转化为圆心与半径的确定上.圆心确定圆的位置,半径确定圆的大小.点与圆上点距离的最大、最小值应首先判断点在圆内还是圆外,然后求这点到圆心的距离. 数形结合是处理解析几何问题常用的方法,一个标准的图形,隐含着丰富的信息,对图形语言要会识别,看懂图形,利用好图形会起到“此时无声胜有声”的效果.如果不利用圆的有关性质来处理,而是设圆上任意一点P(x,y),转化为求|AP|的最大、最小值,问题就变得复杂,所以在处理有关问题时,要选择合适的方式、方法来处理. |


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
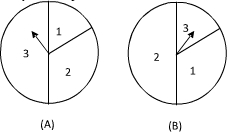 如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ,每一次游戏得到奖励分为ξ
如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ,每一次游戏得到奖励分为ξ查看答案和解析>>
科目:高中数学 来源: 题型:
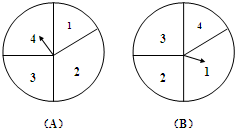 (2010•珠海二模)如图是两个独立的转盘(A)、(B),在两个图中的四个扇形区域的圆心角分别为60°、120°、90°90°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域数为y,x、y∈{1,2,3,4},设x+y的值为ξ,每一次游戏得到奖励分为ξ.
(2010•珠海二模)如图是两个独立的转盘(A)、(B),在两个图中的四个扇形区域的圆心角分别为60°、120°、90°90°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域数为y,x、y∈{1,2,3,4},设x+y的值为ξ,每一次游戏得到奖励分为ξ.查看答案和解析>>
科目:高中数学 来源:全优设计必修二数学苏教版 苏教版 题型:044
解析几何并不是一门独立的学科,很多问题的解决都离不开我们初中学过的平面几何的性质.请想想下面的问题该怎么求解?其中要运用哪些平面几何的知识?
已知圆(x-2)2+y2=1,求点(-2,-3)与圆上的点的距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
|
(Ⅰ)求![]() <2且
<2且![]() >1的概率;
>1的概率;
(Ⅱ)某人进行了12次游戏,求他平均可以得到的奖励分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com