已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,而数列{bn}的首项为1,bn+1-bn-2=0.
(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=an•bn,求数列{cn}的前n项和Tn.
解:(1)∵a
n是S
n与2的等差中项,
∴S
n=2a
n-2,∴a
1=S
1=2a
1-2,解得a
1=2,a
1+a
2=S
2=2a
2-2,解得a
2=4;
(2)∵S
n=2a
n-2①,∴S
n-1=2a
n-1-2(n≥2)②,
①-②得:a
n=2a
n-2a
n-1,即
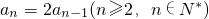
,
∵a
1≠0,∴
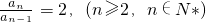
,即数列{a
n}是等比数列.
∵a
1=2,∴
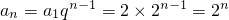
.
由已知得b
n+1-b
n=2,即数列{b
n}是等差数列,
又b
1=1,∴b
n=b
1+(n-1)d=1+2(n-1)=2n-1;
(3)由c
n=a
n•b
n=(2n-1)2
n,
∴
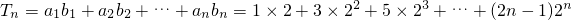
③,
∴
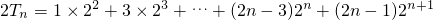
④,
③-④得:
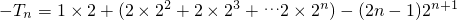
.
即:
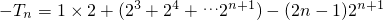
=
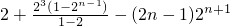
∴
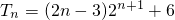
.
分析:(1)由a
n是S
n与2的等差中项得递推式,在递推式中分别取n=1和n=2即可求得a
1和a
2的值;
(2)由(1)中的递推式和求得数列{a
n}是等比数列,由b
n+1-b
n-2=0推得数列{b
n}是等差数列,则数列{a
n},{b
n}的通项公式可求;
(3)把a
n和b
n代入c
n=a
n•b
n后直接利用错位相减法求和.
点评:本题考查了等差数列和等比数列的通项公式,考查了错位相减法求数列的前n项和,求一个等差数列和一个等比数列的积数列的前n项和,常采用错位相减法.此题是中档题.

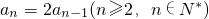 ,
,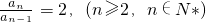 ,即数列{an}是等比数列.
,即数列{an}是等比数列.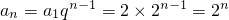 .
.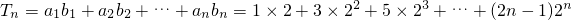 ③,
③,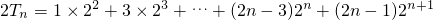 ④,
④,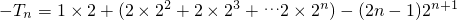 .
.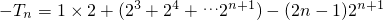 =
=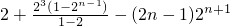
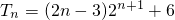 .
.
