
分析 三棱锥P-ABC的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,然后解答即可.
解答 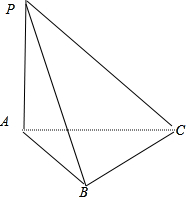 解:如图,在△ABC中,由正弦定理得$\frac{AC}{sinB}=\frac{AB}{sinC}$⇒sinC=$\frac{1}{2}$,∵C<B,∴C=30°,∴A=90°,
解:如图,在△ABC中,由正弦定理得$\frac{AC}{sinB}=\frac{AB}{sinC}$⇒sinC=$\frac{1}{2}$,∵C<B,∴C=30°,∴A=90°,
又∵PA⊥平面ABC,AP,AC,AB两两垂直,
故可将此三棱锥放入一个长、宽、高分别1,$\sqrt{3}$,2$\sqrt{3}$为的长方体内,三棱锥的四个顶点亦为长方体的顶点,其外接球为长方体外接球.
易得外接球半径为$\frac{\sqrt{(2\sqrt{3})^{2}+{1}^{2}+(\sqrt{3})^{2}}}{4}=2$,故外接球表面积为4πR2=16π.
故答案为:16π.
点评 本题考查球的表面积,考查学生空间想象能力,解答的关键是构造球的内接长方体.是基础题


科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -10 | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<a<1 | B. | 0<a<1 | C. | a<-1或a>1 | D. | a=±1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
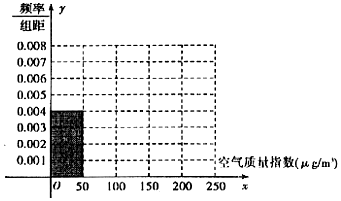
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (1,2] | C. | [1,2] | D. | [1,4] |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:解答题
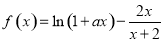 (
(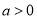 ).
).
(1)当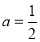 时,求
时,求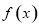 的单调区间;
的单调区间;
(2)若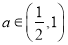 ,
,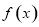 存在两个极值点
存在两个极值点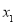 ,
,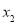 ,试比较
,试比较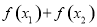 与
与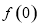 的大小;
的大小;
(3)求证: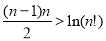 (
(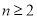 ,
,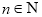 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com