解:(Ⅰ)f′(x)=x
2+(1-a)x-a=(x+1)(x-a),又a>0,
∴当x<-1时,f′(x)>0,f(x)单调递增;当-1<x<a时,f′(x)<0,f(x)单调递减;当x>a时,f′(x)>0,f(x)单调递增.
所以f(x)的单调增区间为:(-∞,-1),(a,+∞);单调减区间为:(-1,a).
(Ⅱ)由(Ⅰ)知f(x)在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,
从而函数f(x)在(-2,0)内恰有两个零点当且仅当

,解得0<a<

.
所以a的取值范围是(0,

).
(Ⅲ)a=1时,f(x)=
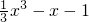
.由(Ⅰ)知f(x)在[-3,-1]上单调递增,在[-1,1]上单调递减,在[1,2]上单调递增.
(1)当t∈[-3,-2]时,t+3∈[0,1],-1∈[t,t+3],f(x)在[t,-1]上单调递增,在[-1,t+3]上单调递减,
因此,f(x)在[t,t+3]上的最大值M(t)=f(-1)=-

,而最小值m(t)为f(t)与f(t+3)中的较小者.
由f(t+3)-f(t)=3(t+1)(t+2)知,当t∈[-3,-2]时,f(t)≤f(t+3),故m(t)=f(t),所以g(t)=f(-1)-f(t).
而f(t)在[-3,-2]上单调递增,因此f(t)≤f(-2)=-

.所以g(t)在[-3,-2]上的最小值为g(-2)=-

-

=

.
(2)当t∈[-2,-1]时,t+3∈[1,2],且-1,1∈[t,t+3].下面比较f(-1),f(1),f(t),f(t+3)的大小.
由f(x)在[-2,-1],[1,2]上单调递增,有f(-2)≤f(t)≤f(-1),f(1)≤f(t+3)≤f(2).
又由f(1)=f(-2)=-

,f(-1)=f(2)=-

,从而M(t)=f(-1)=-

,m(t)=f(1)=-

.
所以g(t)=M(t)-m(t)=

.
综上,函数g(t)在区间[-3,-1]上的最小值为

.
分析:(Ⅰ)由导数与函数单调性的关系解不等式即可;
(Ⅱ)函数f(x)在区间(-2,0)内恰有两个零点,即其图象在(-2,0)内与x轴有两个交点,结合图象可得出f(-2)、f(0)及极值符号,从而可求出a的范围;
(Ⅲ)先求出M(t),m(t),再求出g(t),从而可求得g(t)在[-3,-1]上最小值,其间需要根据极点-1,1所在区间情况分类讨论.
点评:本题考查了应用导数研究函数的单调性、零点以及函数在闭区间上的最值问题,同时考查分析问题、解决问题的能力以及分类讨论的数学思想.

 x3+
x3+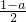 x2-ax-a,其中a>0.
x2-ax-a,其中a>0. ,解得0<a<
,解得0<a< .
. ).
).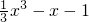 .由(Ⅰ)知f(x)在[-3,-1]上单调递增,在[-1,1]上单调递减,在[1,2]上单调递增.
.由(Ⅰ)知f(x)在[-3,-1]上单调递增,在[-1,1]上单调递减,在[1,2]上单调递增. ,而最小值m(t)为f(t)与f(t+3)中的较小者.
,而最小值m(t)为f(t)与f(t+3)中的较小者. .所以g(t)在[-3,-2]上的最小值为g(-2)=-
.所以g(t)在[-3,-2]上的最小值为g(-2)=- -
- =
= .
. ,f(-1)=f(2)=-
,f(-1)=f(2)=- ,从而M(t)=f(-1)=-
,从而M(t)=f(-1)=- ,m(t)=f(1)=-
,m(t)=f(1)=- .
. .
. .
.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<