抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.
(1)写出该抛物线的方程及其准线方程;
(2)若直线AB与x 轴交于点M(x,0),且y1•y2=-4,求证:点M的坐标为(1,0).
【答案】
分析:(1)由已知可设抛物线方程为y
2=2px.因点P(1,2)在抛物线上,故p=2.由此知所求抛物线的方程是y
2=4x,准线方程是x=-1.
(2)设A(x
1,y
1),B(x
2,y
2).当AB斜率不存在时,y
1=-y
2=2代入y
2=4x,x
1=x
2=1,M(1,0);当AB斜率存在时,设AB:y=k(x-x
)(k≠0),联立
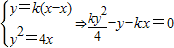
,得M(1,0).
解答:解:(1)由已知可设抛物线方程为y
2=2px.
∵点P(1,2)在抛物线上,∴p=2.
故所求抛物线的方程是y
2=4x,(4分)
准线方程是x=-1.(5分)
(2)设A(x
1,y
1),B(x
2,y
2)
①当AB斜率不存在时,y
1=-y
2=2代入y
2=4x∴x
1=x
2=1,∴M(1,0)(8分)
②当AB斜率存在时,设AB:y=k(x-x
)(k≠0),
联立

∴y
1•y
2=-4x
=-4,∴x
=1,即M(1,0)(12分)
综上:AB直线与x轴交点M(1,0).
点评:本题考查抛物线的方程及其准线方程,解题时要注意抛物线性质的合理运用,仔细审题,注意合理地进行等价转化.

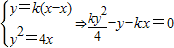 ,得M(1,0).
,得M(1,0).


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案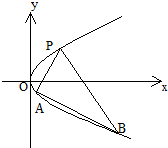 如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.