
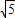 )2+y2=36,定点N(
)2+y2=36,定点N(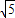 ,0),点P为圆M上的动点,点Q在NP上,点G在MP上,且满足
,0),点P为圆M上的动点,点Q在NP上,点G在MP上,且满足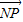 =2
=2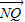 ,
,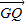 •
•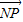 =0.
=0.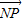 =2
=2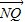 ,
,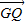 •
•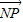 =0,知Q为PN的中点且GQ⊥PN,∴GQ为PN的中垂线,∴|PG|=|GN|,∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,从而可求方程;(Ⅱ)易知-2≤y≤2,从而转化为二次函数求最值.
=0,知Q为PN的中点且GQ⊥PN,∴GQ为PN的中垂线,∴|PG|=|GN|,∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,从而可求方程;(Ⅱ)易知-2≤y≤2,从而转化为二次函数求最值.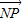 =2
=2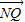 ,
,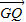 •
•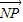 =0,知Q为PN的中点且GQ⊥PN,∴GQ为PN的中垂线,∴|PG|=|GN|
=0,知Q为PN的中点且GQ⊥PN,∴GQ为PN的中垂线,∴|PG|=|GN|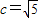 ,∴短半轴长b=2,
,∴短半轴长b=2,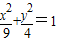
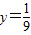 时,2x2+y有最大值18
时,2x2+y有最大值18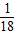 ,当y=-2时,2x2+y有最小值为-2
,当y=-2时,2x2+y有最小值为-2

 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
 )2+y2=
)2+y2=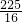 的圆心为M,圆N:(x-
的圆心为M,圆N:(x- )2+y2=的圆心为N,一动圆与圆M内切,与圆N外切.
)2+y2=的圆心为N,一动圆与圆M内切,与圆N外切.查看答案和解析>>
科目:高中数学 来源:0128 模拟题 题型:解答题
 )2+y2=36,定点N(
)2+y2=36,定点N( ,0),点P为圆M上的动点,点Q在NP上,点G在MP上,且满足
,0),点P为圆M上的动点,点Q在NP上,点G在MP上,且满足 。
。 是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由。
是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由。查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东聊城市东阿县曹植培训学校高三(上)12月月考数学试卷(解析版) 题型:解答题
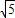 )2+y2=36,定点N(
)2+y2=36,定点N(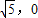 ),点P为圆M上的动点,点G在MP上,且满足|GP|=|GN|
),点P为圆M上的动点,点G在MP上,且满足|GP|=|GN|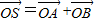 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.查看答案和解析>>
科目:高中数学 来源:2011年福建省厦门市双十中学高考考前热身数学试卷(理科)(解析版) 题型:解答题
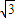 )2+y2=
)2+y2=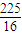 的圆心为M,圆N:(x-
的圆心为M,圆N:(x-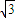 )2+y2=的圆心为N,一动圆与圆M内切,与圆N外切.
)2+y2=的圆心为N,一动圆与圆M内切,与圆N外切.查看答案和解析>>
科目:高中数学 来源:2013年北京市海淀区高考数学一模试卷(理科)(解析版) 题型:解答题
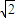 )2+y2=r2=r2(r>0).若椭圆C:
)2+y2=r2=r2(r>0).若椭圆C: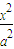 +
+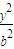 =1(a>b>0)的右顶点为圆M的圆心,离心率为
=1(a>b>0)的右顶点为圆M的圆心,离心率为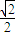 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com