
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求b的值;
(2)用定义法证明函数f(x)在R上是减函数;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
【答案】
(1)解:∵定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
∴f(0)= ![]() =0,解得b=1
=0,解得b=1
(2)解:由(1)可得:f(x)= ![]() =
= ![]() .
.
x1<x2,则 ![]() >0,
>0,
∴f(x1)﹣f(x2)= ![]() =
= ![]() >0,
>0,
∴f(x1)>f(x2).
∴函数f(x)在R上是减函数
(3)解:∵函数f(x)是R上的奇函数,对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,
∴f(t2﹣2t)<﹣f(2t2﹣k)=f(k﹣2t2),
∵函数f(x)在R上是减函数,
∴t2﹣2t>k﹣2t2,
∴k<3t2﹣2t= ![]() ,任意的t∈R恒成立.
,任意的t∈R恒成立.
∴k ![]() .
.
因此k的取值范围是 ![]()
【解析】(1)利用f(0)=0即可解出;(2)利用减函数的定义即可证明;(3)利用函数的奇偶性、单调性即可解出.
【考点精析】根据题目的已知条件,利用函数单调性的判断方法和函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】设x,y满足不等式组  ,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
A.[﹣1,2]
B.[﹣2,1]
C.[﹣3,﹣2]
D.[﹣3,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
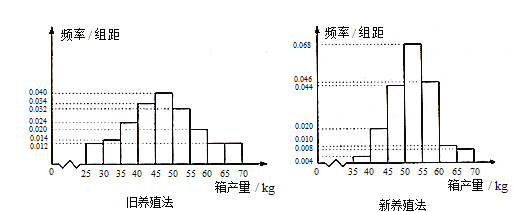
(1) 记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2) 填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3) 根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。
附:
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的各项都为正数,其前n项和为Sn , 已知4Sn=an2+2an .
(1)求a1级数列{an}的通项公式;
(2)设数列{bn}前n项和为Tn , 且bn= ![]() ,若λTn<n+(﹣1)n36对n∈N*恒成立,求实数λ的取值范围.
,若λTn<n+(﹣1)n36对n∈N*恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cos2x,sinx),
=(2cos2x,sinx), ![]() =(1,2cosx). (Ⅰ)若
=(1,2cosx). (Ⅰ)若 ![]() ⊥
⊥ ![]() 且0<x<π,试求x的值;
且0<x<π,试求x的值;
(Ⅱ)设f(x)= ![]()
![]() ,试求f(x)的对称轴方程和对称中心.
,试求f(x)的对称轴方程和对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB= ![]() ,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( ) 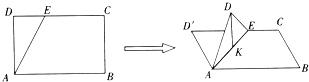
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,BC⊥平面APC,AB=2 ![]() ,AP=PC=CB=2.
,AP=PC=CB=2. 
(1)求证:AP⊥平面PBC;
(2)求二面角P﹣AB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )过点
)过点![]() ,
, ![]() 、
、![]() 分别为其左、右焦点,
分别为其左、右焦点, ![]() 为坐标原点,点
为坐标原点,点![]() 为椭圆上一点,
为椭圆上一点, ![]() 轴,且
轴,且![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的离心率和方程;
的离心率和方程;
(Ⅱ)设![]() 、
、![]() 是椭圆上两动点,若直线
是椭圆上两动点,若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com