已知△ABC是边长为3,4,5的直角三角形,点P是此三角形内切圆上一动点,分别以PA、PB、PC为直径作圆,则这三个圆的面积之和的最大值与最小值的和为( )
A.12π
B.10π
C.8π
D.6π
【答案】
分析:由△ABC是边长为3,4,5的直角三角形,点P是此三角形内切圆上一动点,建立平面直角坐标系,求三个圆的面积之和的最大值与最小值的和,转化为点P到三角形三个定点的距离的平方和的最值问题.
解答:解:建立坐标系 设A(3,0),B(0,4),C(0,0),P(x,y),△ABC内切圆半径为r.
∵三角形ABC面积 S=

AB×AC=

(AB+AC+BC)r=12,解得 r=1
即内切圆圆心坐标为 (1,1)
∵P在内切圆上
∴(x-1)
2+(y-1)
2=1
∵P点到A,B,C距离的平方和为 d=x
2+y
2+(x-3)
2+y
2+x
2+(y-4)
2=3(x-1)
2+3(y-1)
2-2y+19=22-2y
显然 0≤y≤2 即 18≤d≤22,
∴

即以PA,PB,PC为直径的三个圆面积之和最大值为

最小值为
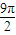
.
故选B.
点评:考查了解析法求最值,求三个圆的面积之和的最大值与最小值的和转化为点P到三角形三个定点的距离的平方和的最值问题,体现了转化的思想方法.

 AB×AC=
AB×AC= (AB+AC+BC)r=12,解得 r=1
(AB+AC+BC)r=12,解得 r=1 即以PA,PB,PC为直径的三个圆面积之和最大值为
即以PA,PB,PC为直径的三个圆面积之和最大值为 最小值为
最小值为 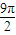 .
.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案