
【题目】如表是我国2012年至2018年国内生产总值(单位:万亿美元)的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
国内生产总值 (单位:万亿美元) | 8.5 | 9.6 | 10.4 | 11 | 11.1 | 12.1 | 13.6 |
(1)从表中数据可知![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程;
为预报变量的线性回归方程;
(2)已知美国2018年的国内生产总值约为20.5万亿美元,用(1)的结论,求出我国最早在那个年份才能赶上美国2018年的国内生产总值?
参考数据:![]() ,
,
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
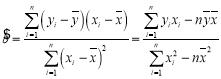 ,
,![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,点C在以AB为直径的圆上运动,PA⊥平面ABC,且PA=AC,D,E分别是PC,PB的中点.
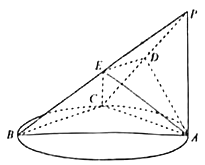
(1)求证:PC⊥平面ADE.
(2)若二面角C﹣AE﹣B为60°,求直线AB与平面ADE所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所开发了一种新药,测得成人注射该药后血药浓度y(微克/毫升)与给药时间x(小时)之间的若干组数据,并由此得出y与x之间的一个拟合函数y=40(0.6x﹣0.62x)(x∈[0,12]),其简图如图所示.试根据此拟合函数解决下列问题:

(1)求药峰浓度与药峰时间(精确到0.01小时),并指出血药浓度随时间的变化趋势;
(2)求血药浓度的半衰期(血药浓度从药峰浓度降到其一半所需要的时间)(精确到0.01小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】基于移动网络技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,给人们带来新的出行体验,某共享单车运营公司的市场研究人员为了了解公司的经营状况,对公司最近6个月的市场占有率![]() 进行了统计,结果如下表:
进行了统计,结果如下表:
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
(1)请用相关系数说明能否用线性回归模型拟合![]() 与月份代码
与月份代码![]() 之间的关系.如果能,请计算出
之间的关系.如果能,请计算出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)根据调研数据,公司决定再采购一批单车扩大市场,从成本1000元/辆的![]() 型车和800元/辆的
型车和800元/辆的![]() 型车中选购一种,两款单车使用寿命频数如下表:
型车中选购一种,两款单车使用寿命频数如下表:
| 1年 | 2年 | 3年 | 4年 | 总计 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
经测算,平均每辆单车每年能为公司带来500元的收入,不考虑除采购成本以外的其它成本,假设每辆单车的使用寿命都是整数年,用频率估计每辆车使用寿命的概率,以平均每辆单车所产生的利润的估计值为决策依据,如果你是公司负责人,会选择哪款车型?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数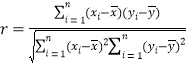 ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的两条直线,与抛物线分别相交于点
作互相垂直的两条直线,与抛物线分别相交于点![]() ,
,![]() 、
、![]() 分别为弦
分别为弦![]() 、
、![]() 的中点,求
的中点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案①:规定每日底薪50元,快递业务每完成一单提成3元;方案②:规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元.该快餐连锁店记录了每天骑手的人均业务量.现随机抽取100天的数据,将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,整理得到如图所示的频率分布直方图.
七组,整理得到如图所示的频率分布直方图.
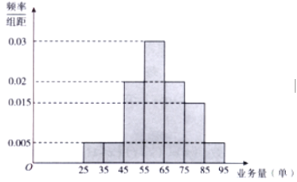
(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)若骑手甲、乙选择了日工资方案①,丙、丁选择了日工资方案②.现从上述4名骑手中随机选取2人,求至少有1名骑手选择方案①的概率;
(3)若从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() ,(
,(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴的 非负半轴为极轴建立极坐标系,曲线
轴的 非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1(-
(a>b>0)的两个焦点分别为F1(-![]() ,0)、F2(
,0)、F2(![]() ,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程;
(2)已知点N的坐标为(3,2),点P的坐标为(m,n)(m≠3).过点M任作直线l与椭圆C相交于A、B两点,设直线AN、NP、BN的斜率分别为k1、k2、k3,若k1+k3=2k2,试求m,n满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第二届乌镇互联网大会中,为了提高安保的级别同时又为了方便接待,现将其中的五个参会国的人员安排酒店住宿,这五个参会国要在![]() 、
、![]() 、
、![]() 三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有_________(填具体数字)
三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有_________(填具体数字)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com