
【题目】(Ⅰ)求不等式﹣x2﹣2x+3<0的解集(用集合或区间表示) (Ⅱ)求不等式|x﹣3|<1的解集(用集合或区间表示)
【答案】解:(Ⅰ)不等式﹣x2﹣2x+3<0可化为. x2+2x﹣3>0,…
即(x+3)(x﹣1)>0,
解得或x<﹣3或x>1,
所以不等式的解集为{x|x<﹣3或x>1};
(Ⅱ)不等式|x﹣3|<1可化为
﹣1<x﹣3<1,
解得2<x<4,
所以不等式的解集为{x|2<x<4}.
【解析】(Ⅰ)根据一元二次不等式的解法步骤求解即可;(Ⅱ)利用绝对值的定义化简不等式,求解即可.
【考点精析】本题主要考查了解一元二次不等式的相关知识点,需要掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() :
: ![]() 相交于
相交于![]() ,
, ![]() 两点,
两点, ![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() .
.
(Ⅰ)证明:抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 平行;
平行;
(Ⅱ)是否存在实数![]() 使
使![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂每日生产一种大型产品1件,每件产品的投入成本为2000元.产品质量为一等品的概率为![]() ,二等品的概率为
,二等品的概率为![]() ,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
(1)求在连续生产3天中,恰有一天生产的两件产品都为一等品的的概率;
(2)已知该厂某日生产的2件产品中有一件为一等品,求另一件也为一等品的概率;
(3)求该厂每日生产该种产品所获得的利润![]() (元)的分布列及数学期望.
(元)的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的极值点,且直线
的极值点,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2+y2﹣ax+y+1=0表示圆;命题q:方程2ax+(1﹣a)y+1=0表示斜率大于1的直线,若p∨q为真命题,p∧q为假命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种零件按质量标准分为1,2,3,4,5五个等级,现从一批该零件巾随机抽取20个,对其等级进行统计分析,得到频率分布表如下
等级 | 1 | 2 | 3 | 4 | 5 |
频率 | 0.05 | m | 0.15 | 0.35 | n |
(1)在抽取的20个零件中,等级为5的恰有2个,求m,n;
(2)在(1)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级恰好相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1 , F2是双曲线C: ![]() (a>0,b>0)的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若△ABF2为等边三角形,则双曲线的离心率为( )
(a>0,b>0)的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若△ABF2为等边三角形,则双曲线的离心率为( ) 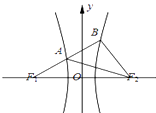
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知条件p:x2﹣3x﹣4≤0;条件q:x2﹣6x+9﹣m2≤0,若p是q的充分不必要条件,则m的取值范围是( )
A.[﹣1,1]
B.[﹣4,4]
C.(﹣∞,﹣1]∪[1,+∞)
D.(﹣∞,﹣4]∪[4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为 ![]() ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为(32Q+3)150%+x50%,而当年产销量相等.
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为(32Q+3)150%+x50%,而当年产销量相等.
(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com